Pearson의 상관 계수
공식
두 변수 사이의 선형 관계를 측정합니다. 상관 계수의 값은 −1과 +1 사이로 가정합니다. 한 변수가 증가할 때 다른 변수는 감소하는 경향이 있으면 상관 계수는 음수입니다. 반대로 두 변수가 함께 증가하는 경향이 있으면 상관 계수는 양수입니다.
변수 x 및 y에 대해:
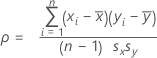
표기법
| 용어 | 설명 |
|---|---|
 | 첫 번째 변수에 대한 표본 평균 |
| sx | 첫 번째 변수에 대한 표본 표준 편차 |
 | 두 번째 변수에 대한 표본 평균 |
| sy | 두 번째 변수에 대한 표본 표준 편차 |
| n | 관측치 수 |
Pearson의 상관 계수 신뢰 구간
ρ의 (1− α)100% 양측 신뢰 구간은 (ρL, ρU)이며, 여기서 하한인 ρL과 상한인 ρU는 다음을 따릅니다.
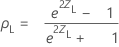
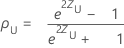
설명:


표기법
| 용어 | 설명 |
|---|---|
| r | 알 수 없는 상관 ρ의 Pearson 표본 상관 추정치 |
| ρ | 상관 계수 |
| n | 관측치 수 |
Spearman의 상관 계수
Spearman의 상관 계수와 p-값을 계산하려면 데이터 순위에 대해 Pearson 상관을 수행하십시오. 같은 값을 갖는 반응의 순위는 같은 값의 순위에 대한 평균입니다. 다음 표는 두 데이터 표본에 대한 순위를 보여줍니다.
| C1 | C2 | C3 | C4 |
|---|---|---|---|
| A | 순위 A | B | 순위 B |
| 45 | 4 | 23 | 1 |
| 78 | 6 | 25 | 3 |
| 24 | 3 | 25 | 3 |
| 51 | 5 | 25 | 3 |
| 13 | 1.5 | 34 | 6 |
| 13 | 1.5 | 30 | 5 |
A와 B 간의 Spearman 상관 계수는 −0.678이고 p-값은 0.139입니다. 이 값들은 순위 A와 순위 B의 값에 대한 Pearson 상관의 계수와 p-값과 동일합니다.
Minitab에서는 하나 또는 두 변수 모두의 결측 데이터가 포함된 행을 계산에서 제외합니다. 두 열의 행 수는 모두 같아야 합니다.
Spearman의 상관 계수 신뢰 구간
ρ의 (1− α)100% 양측 신뢰 구간은 (ρL, ρU)이며, 여기서 하한인 ρL과 상한인 ρU는 다음을 따릅니다.
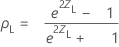
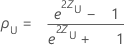
설명:


Bonnett과 Wright(2000)는 표준 오차에 대해 다음과 같은 조정을 제안합니다.

표기법
| 용어 | 설명 |
|---|---|
| r | 알 수 없는 상관 ρ의 Spearman 표본 상관 추정치 |
| ρ | 상관 계수 |
| n | 변수 쌍에 대해 결측 데이터가 없는 데이터의 행 수 |
p-값
상관이 0이라는 검정에 대한 가설은 다음과 같습니다.
H0: ρ = 0 대 H1: ρ ≠ 0. 여기서 ρ는 변수 한 쌍 사이의 Pearson 상관 계수이거나 Spearman 상관 계수입니다.
공식
Pearson 상관 계수와 Spearman 상관 계수의 검정 통계량의 공식은 다음과 같이 동일합니다.

p-값은 2 × P(T > t)이며, 여기서 T는 자유도가 n – 2인 t 분포를 따릅니다.
표기법
| 용어 | 설명 |
|---|---|
| r | 표본 상관 계수 |
| n | 관측치 수 |
