한 건강 관리 컨설턴트가 두 병원의 환자 만족도 등급을 비교하려고 합니다. 이 컨설턴트는 각 병원에 대해 환자 20명의 만족도 점수를 수집합니다.
컨설턴트는 두 병원의 환자 등급의 표준 편차가 다른지 여부를 확인하기 위해 두 표본 분산 검정을 수행합니다.
- 표본 데이터를 엽니다 병원비교.MWX#.
- 을 선택합니다.
- 드롭다운 리스트에서 두 표본이 모두 한 열에 있음을 선택합니다.
- 표본에 등급을 입력합니다.
- 표본 ID에 병원을 입력합니다.
- 확인을(를) 클릭합니다.
결과 해석
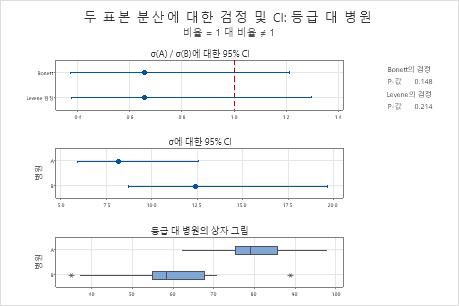
귀무 가설은 표준 편차 간의 비율이 1이라는 것입니다 두 p-값이 모두 유의 수준(α 또는 알파로 표시됨) 0.05보다 크기 때문에 컨설턴트는 귀무 가설을 기각할 수 없습니다. 컨설턴트는 병원 간의 표준 편차가 다르다는 결론을 내릴 수 있는 충분한 증거가 없습니다.
방법
| σ₁: 병원 = A일 때 등급의 표준 편차 |
|---|
| σ₂: 병원 = B일 때 등급의 표준 편차 |
| 비율: σ₁/σ₂ |
| Bonett과 Levene의 방법은 모든 계량형 분포에 유효합니다. |
기술 통계량
| 병원 | N | 표준 편차 | 분산 | σ에 대한 95% CI |
|---|---|---|---|---|
| A | 20 | 8.183 | 66.958 | (5.893, 12.597) |
| B | 20 | 12.431 | 154.537 | (8.693, 19.709) |
표준 편차의 비율
| 추정 비율 | Bonett을 사용한 비율에 대한 95% CI | Levene을 사용한 비율에 대한 95% CI |
|---|---|---|
| 0.658241 | (0.372, 1.215) | (0.378, 1.296) |
검정
| 귀무 가설 | H₀: σ₁ / σ₂ = 1 |
|---|---|
| 대립 가설 | H₁: σ₁ / σ₂ ≠ 1 |
| 유의 수준 | α = 0.05 |
| 방법 | 검정 통계량 | DF1 | DF2 | P-값 |
|---|---|---|---|---|
| Bonett | 2.09 | 1 | 0.148 | |
| Levene 검정 | 1.60 | 1 | 38 | 0.214 |