원하는 방법 또는 공식을 선택하십시오.
이 항목의 내용
신뢰 구간(CI)
공식
~ 
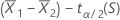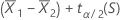
표기법
| 용어 | 설명 |
|---|---|
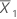 | 첫 번째 표본의 평균 |
 | 두 번째 표본의 평균 |
| tα/2 | 1 – α/2에서 t 분포의 역 누적 확률 |
| α | 1 – 신뢰 수준 / 100 |
| s | 검정 통계량에 대해 계산된 표본 표준 편차 |
T-값
공식
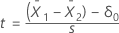
s는 
의 표본 표준 편차로, 분산 가정에 따라 달라집니다.
의 표본 표준 편차로, 분산 가정에 따라 달라집니다.
- 이분산
-
이분산을 가정하는 경우
의 표본 표준 편차는 다음과 같습니다.
자유도는 다음과 같습니다.
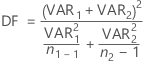
필요한 경우 Minitab에서는 자유도를 정수로 자릅니다.(이는 반올림보다 더 보수적인 방법입니다.)
- 등분산
-
등분산을 가정하는 경우 공통 분산은 합동 분산에 의해 추정됩니다.
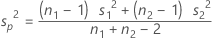
의 표준 편차는 다음과 같이 추정됩니다.
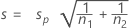
검정 통계량 자유도는 다음과 같습니다.
DF = n1 + n2 – 2
표기법
| 용어 | 설명 |
|---|---|
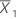 | 첫 번째 표본의 평균 |
 | 두 번째 표본의 평균 |
| s |  의 표본 표준 편차 |
| δ0 | 두 모집단 평균 간의 귀무 가설에서의 차이 |
| s1 | 첫 번째 표본의 표본 표준 편차 |
| s2 | 두 번째 표본의 표본 표준 편차 |
| n1 | 첫 번째 표본의 표본 크기 |
| n2 | 두 번째 표본의 표본 크기 |
| VAR1 |  |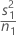
| VAR2 |  |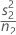
합동 표준 편차 계산
C1에 반응값이 있고 C3에 각 요인 수준에 대한 평균이 있다고 가정합니다. 예:
| C1 | C2 | C3 |
|---|---|---|
| 반응값 | 요인 | 평균 |
| 18.95 | 1 | 14.5033 |
| 12.62 | 1 | 14.5033 |
| 11.94 | 1 | 14.5033 |
| 14.42 | 2 | 10.5567 |
| 10.06 | 2 | 10.5567 |
| 7.19 | 2 | 10.5567 |
- 를 선택합니다.
- 다음 변수에 결과 저장에 C4를 입력합니다.
- 식에 SQRT((SUM((C1 - C3)**2)) / (총 관측치 수 - 그룹 수))를 입력합니다. 위의 예에서 합동 표준 편차 식은 SQRT((SUM(('반응값' - '평균')**2)) / (6 - 2))입니다.
3.75489 값이 저장됩니다.
p-값
공식
p-값은 대립 가설에 따라 다르게 계산됩니다.
| 대립 가설 | p-값 |
|---|---|
 |
 |
 |
 |
 |
 |
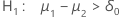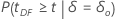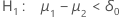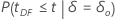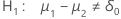자유도 DF는 분산 가정에 따라 달라집니다.
- 이분산
-
이분산을 가정하는 경우 자유도는 다음과 같습니다.
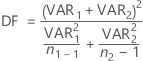
필요한 경우 Minitab에서는 자유도를 정수로 자릅니다.(이는 반올림보다 더 보수적인 방법입니다.)
- 등분산
-
등분산을 가정하는 경우 검정 통계량 자유도는 다음과 같습니다.
DF = n1 + n2 – 2
표기법
| 용어 | 설명 |
|---|---|
| μ1 | 첫 번째 표본의 모집단 평균 |
| μ1 | 두 번째 표본의 모집단 평균 |
| n1 | 첫 번째 표본의 표본 크기 |
| n2 | 두 번째 표본의 표본 크기 |
| δ0 | 두 모집단 평균 간의 귀무 가설에서의 차이 |
| t | 표본 데이터의 t-통계량 |
| t | 자유도 DF인 t-분포를 따르는 랜덤 변수 |
| VAR1 |  |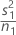
| VAR2 |  |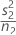
