이 항목의 내용
통계량
| 용어 | 설명 |
|---|---|
| 표본 i의 발생률 |
 |
| 용어 | 설명 |
|---|---|
| 표본 i의 평균 발생 횟수 |
 |
정규 근사 방법의 비율의 차이에 대한 가설 검정
공식
정규 근사 검정은 귀무 가설 하에서 근사적으로 표준 정규 분포를 따르는 다음 Z-통계량을 기반으로 합니다.
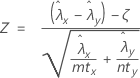
Minitab에서는 각 대립 가설에 대해 다음과 같은 p-값 방정식을 사용합니다.
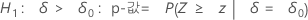
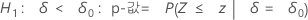
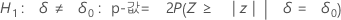
표기법
| 용어 | 설명 |
|---|---|
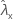 | 표본 X에 대한 비율의 관측치 |
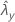 | 표본 Y에 대한 비율의 관측치 |
| ζ | 두 표본의 모집단 비율 간 차이의 실제 값 |
| ζ0 | 두 표본의 모집단 비율 간 차이의 귀무 가설에서의 값 |
| m | 표본 X의 표본 크기 |
| n | 표본 Y의 표본 크기 |
| tx | 표본 X의 길이 |
| ty | 표본 Y의 길이 |
정확한 방법의 비율의 차이에 대한 가설 검정
공식
귀무 가설에서의 차이가 0과 같은 경우 Minitab에서는 정확 검정을 사용하여 다음과 같은 귀무 가설을 검정합니다.
H0: ζ = λx – λy = 0 또는 H0: λx = λy
정확 검정은 다음과 같은 사실을 기반으로 하며, 귀무 가설이 참이라고 가정합니다.
S | W ~ Binomial(w, p)
설명:


W = S + U


-
H1: ζ > 0: p-값 = P(S ≥ s | w = s + u, p = p0)
-
H1: ζ < 0: p-값 = P(S ≤ s | w = s + u, p = p0)
- H1: ζ ≠ 0:
- P(S ≤ s | w = s + u, p = p0) ≤ 0.5 또는 P(S ≥ s | w = s + u, p = p0) ≤ 0.5인 경우
p-값 = 2 × min {P(S ≤ s | w = s + u, p = p0), P(S ≥ s | w = s + u, p = p0)}
- 그렇지 않은 경우, p-값 = 1.0
- P(S ≤ s | w = s + u, p = p0) ≤ 0.5 또는 P(S ≥ s | w = s + u, p = p0) ≤ 0.5인 경우
설명:

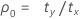
표기법
| 용어 | 설명 |
|---|---|
 | 표본 X에 대한 비율의 관측치 |
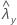 | 표본 Y에 대한 비율의 관측치 |
| λx | 모집단 X에 대한 비율의 실제 값 |
| λy | 모집단 Y에 대한 비율의 실제 값 |
| ζ | 두 표본의 모집단 비율 간 차이의 실제 값 |
| tx | 표본 X의 길이 |
| ty | 표본 Y의 길이 |
| m | 표본 X의 표본 크기 |
| n | 표본 Y의 표본 크기 |
합동 비율 방법을 사용한 비율의 차이에 대한 가설 검정
다음 귀무 가설을 사용하여 차이 0을 검정하는 경우 두 표본 모두에 대한 합동 비율을 사용할 수 있습니다.

공식
합동-비율 검정은 다음 귀무 가설 하에서 근사적으로 표준 정규 분포를 따르는 다음 Z-통계량을 기반으로 합니다.
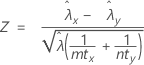
설명:
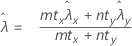
Minitab에서는 각 대립 가설에 대해 다음과 같은 p-값 방정식을 사용합니다.
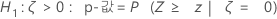
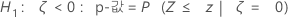
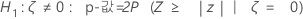
표기법
| 용어 | 설명 |
|---|---|
 | 표본 X에 대한 비율의 관측치 |
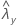 | 표본 Y에 대한 비율의 관측치 |
| λx | 모집단 X에 대한 비율의 실제 값 |
| λy | 모집단 Y에 대한 비율의 실제 값 |
| ζ | 두 표본의 모집단 비율 간 차이의 실제 값 |
| m | 표본 X의 표본 크기 |
| n | 표본 Y의 표본 크기 |
| tx | 표본 X의 길이 |
| ty | 표본 Y의 길이 |
정규 근사 방법의 평균의 차이에 대한 가설 검정
공식
정규 근사 검정은 귀무 가설 하에서 근사적으로 표준 정규 분포를 따르는 다음 Z-통계량을 기반으로 합니다.
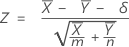
Minitab에서는 각 대립 가설에 대해 다음과 같은 p-값 방정식을 사용합니다.
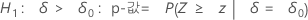
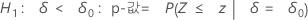
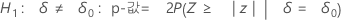
표기법
| 용어 | 설명 |
|---|---|
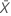 | 표본 X의 평균 발생 횟수의 관측치 |
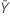 | 표본 Y의 평균 발생 횟수의 관측치 |
| δ | 두 표본의 모집단 평균 간 차이의 실제 값 |
| δ 0 | 두 표본의 모집단 평균 간 차이의 귀무 가설에서의 값 |
| m | 표본 X의 표본 크기 |
| n | 표본 Y의 표본 크기 |
정확한 방법의 평균의 차이에 대한 가설 검정
공식

정확 검정은 다음과 같은 사실을 기반으로 하며, 귀무 가설이 참이라고 가정합니다.
S | W ~ Binomial(w, p)
설명:


W = S + U
Minitab에서는 각 대립 가설에 대해 다음과 같은 p-값 방정식을 사용합니다.
H1: δ > 0: p-값 = P(S ≥ s | w = s + u, δ = 0)
H1: δ < 0: p-값 = P(S ≤ s | w = s + u, δ = 0)
-
P(S ≤ s|w = s + u, δ = 0) ≤ 0.5
또는 P(S ≥ s|w = s + u, δ = 0) ≤ 0.5인
경우

- 그렇지 않은 경우, p-값 = 1.0
m = n이 아닌 경우 양쪽 꼬리 검정은 꼬리가 같은 검정이 아닙니다.
표기법
| 용어 | 설명 |
|---|---|
| μx | 모집단 X의 평균 발생 횟수의 실제 값 |
| μy | 모집단 Y의 평균 발생 횟수의 실제 값 |
| δ | 두 표본의 모집단 평균 간 차이의 실제 값 |
| m | 표본 X의 표본 크기 |
| n | 표본 Y의 표본 크기 |
합동 평균 방법의 평균의 차이에 대한 가설 검정
공식

합동-평균 검정은 다음 귀무 가설 하에서 근사적으로 표준 정규 분포를 따르는 다음 Z 값을 기반으로 합니다.
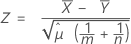
설명:
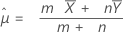
Minitab에서는 각 대립 가설에 대해 다음과 같은 p-값 방정식을 사용합니다.



표기법
| 용어 | 설명 |
|---|---|
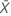 | 표본 X의 평균 발생 횟수의 관측치 |
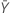 | 표본 Y의 평균 발생 횟수의 관측치 |
| µx | 모집단 X의 평균 발생 횟수의 실제 값 |
| µy | 모집단 Y의 평균 발생 횟수의 실제 값 |
| δ | 두 표본의 모집단 평균 간 차이의 실제 값 |
| m | 표본 X의 표본 크기 |
| n | 표본 Y의 표본 크기 |
비율의 차이에 대한 신뢰 구간
공식
두 모집단 포아송 비율 간의 차이에 대한 100(1 – α)% 신뢰 구간은 다음과 같이 계산됩니다.
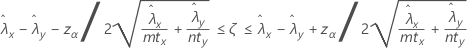
표기법
| 용어 | 설명 |
|---|---|
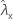 | 표본 X에 대한 비율의 관측치 |
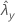 | 표본 Y에 대한 비율의 관측치 |
| ζ | 두 표본의 모집단 비율 간 차이의 실제 값 |
| zx | 표준 정규 분포의 상위 x 백분위수 점, 여기서 0 < x < 1 |
| m | 표본 X의 표본 크기 |
| n | 표본 Y의 표본 크기 |
| tx | 표본 X의 길이 |
| ty | 표본 Y의 길이 |
비율의 차이에 대한 신뢰 구간
공식
"보다 큼" 검정을 지정하는 경우 두 모집단 포아송 비율 간의 차이에 대한 100(1 – α)% 신뢰 하한은 다음과 같이 계산됩니다.
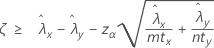
"보다 작음" 검정을 지정하는 경우 두 모집단 포아송 비율 간의 차이에 대한 100(1 – α)% 신뢰 상한은 다음과 같이 계산됩니다.
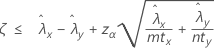
표기법
| 용어 | 설명 |
|---|---|
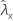 | 표본 X에 대한 비율의 관측치 |
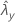 | 표본 Y에 대한 비율의 관측치 |
| ζ | 두 표본의 모집단 비율 간 차이의 실제 값 |
| zx | 표준 정규 분포의 상위 x 백분위수 점, 여기서 0 < x < 1 |
| m | 표본 X의 표본 크기 |
| n | 표본 Y의 표본 크기 |
| tx | 표본 X의 길이 |
| ty | 표본 Y의 길이 |
평균의 차이에 대한 신뢰 구간
공식
두 모집단 포아송 평균 간의 차이에 대한 100(1 – α)% 신뢰 구간은 다음과 같이 계산됩니다.
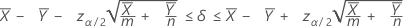
표기법
| 용어 | 설명 |
|---|---|
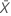 | 표본 X의 평균 발생 횟수의 관측치 |
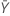 | 표본 Y의 평균 발생 횟수의 관측치 |
| δ | 두 표본의 모집단 평균 간 차이의 실제 값 |
| zx | 표준 정규 분포의 상위 x 백분위수 점, 여기서 0 < x < 1 |
| m | 표본 X의 표본 크기 |
| n | 표본 Y의 표본 크기 |
평균의 차이에 대한 신뢰 구간
공식
"보다 큼" 검정을 지정하는 경우 두 모집단 포아송 평균 간의 차이에 대한 100(1 – α)% 신뢰 하한은 다음과 같이 계산됩니다.
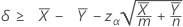
"보다 작음" 검정을 지정하는 경우 두 모집단 포아송 평균 간의 차이에 대한 100(1 – α)% 신뢰 상한은 다음과 같이 계산됩니다.
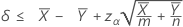
표기법
| 용어 | 설명 |
|---|---|
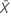 | 표본 X의 평균 발생 횟수의 관측치 |
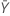 | 표본 Y의 평균 발생 횟수의 관측치 |
| δ | 두 표본의 모집단 평균 간 차이의 실제 값 |
| zx | 표준 정규 분포의 상위 x 백분위수 점, 여기서 0 < x < 1 |
| m | 표본 X의 표본 크기 |
| n | 표본 Y의 표본 크기 |
