원하는 방법 또는 공식을 선택하십시오.
이 항목의 내용
신뢰 구간(CI)
공식
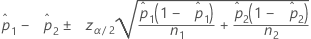
표기법
| 용어 | 설명 |
|---|---|
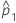 | 첫 번째 모집단 비율의 추정치 |
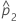 | 두 번째 모집단 비율의 추정치 |
| n1 | 첫 번째 표본의 시행 횟수 |
| n2 | 두 번째 표본의 시행 횟수 |
| zα/2 | 1 – α/2에서 표준 정규 분포의 역 누적 확률. |
| α | 1 – 신뢰 수준/100 |
정규 근사 검정
검정 통계량 Z의 계산은 p를 추정하기 위해 사용되는 방법에 따라 다릅니다.
- p의 별도 추정치
- 기본적으로 Minitab에서는 각 모집단에 대해 p의 별도 추정치를 사용하여 다음과 같이 Z를 계산합니다.
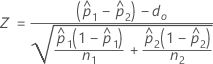
- p의 합동 추정치
- 귀무 가설에서의 검정 차이가 0이고 검정에 대해 p의 합동 추정치를 사용하는 경우 Minitab에서는 다음과 같이 Z를 계산합니다.
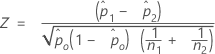
각 대립 가설에 대한 p-값은 다음과 같습니다.
- H1: p1 > p2 : p-값 = P(Z1 ≥ z)
- H1: p1 < p2 : p-값 = P(Z1 ≤ z)
- H1: p1 ≠ p2 : p-값 = 2P(Z1 ≥ z)
표준 정규 분포에 대한 확률을 계산합니다.
표기법
| 용어 | 설명 |
|---|---|
| p1 | 첫 번째 모집단 내 사건의 실제 비율 |
| p2 | 두 번째 모집단 내 사건의 실제 비율 |
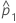 | 첫 번째 표본 내 사건의 관측 비율 |
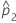 | 두 번째 표본 내 사건의 관측 비율 |
| n1 | 첫 번째 표본의 시행 횟수 |
| n2 | 두 번째 표본의 시행 횟수 |
| d0 | 첫 번째 비율과 두 번째 비율 간 귀무 가설에서의 차이 |
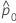 | 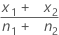 |
| x1 | 첫 번째 표본의 사건 수 |
| x2 | 두 번째 표본의 사건 수 |
Fisher의 정확 검정
Minitab에서는 정규 근사에 기초한 검정 외에 Fisher의 정확 검정을 수행합니다. Fisher의 정확 검정은 모든 표본 크기에 대해 유효합니다.
공식
귀무 가설 하에서 첫 번째 표본(x1)의 사건 수는 모수가 다음과 같은 초기하 분포를 따릅니다.
- 모집단 크기 = n1 + n2
- 모집단 내 사건 수 = x1 + x2
- 표본 크기 = n1
f( )와 F( )를 각각 초기하 분포의 PDF와 CDF로 설정합니다. 최빈값은 초기하 분포의 최빈값으로 설정합니다. 각 대립 가설에 대한 p-값은 다음과 같습니다.
- H1: p1 < p2
p-값 = F(x1)
- H1: p1 > p2
p-값 = 1 – F(x1 – 1)
- H1: p1 ≠ p2
다음과 같은 세 가지 경우가 존재합니다.
- 경우 1: x1 < 최빈값
p-값 = p-하한 + p-상한
용어 설명 p-하한 F(x1) p-상한 1 – F(y – 1) y f(y) <f(x1)인 최빈값보다 큰 가장 작은 정수 참고
p-상한은 0일 수도 있습니다.
- 경우 2: x1 = 최빈값
p-값 = 1.0
- 경우 3: x1 > 최빈값
p-값 = p-하한 + p-상한
용어 설명 p-상한 1 – F(x1 – 1) p-하한 F(y) y f(y) < f(x1)인 최빈값보다 작은 가장 큰 정수 참고
p-하한은 0일 수도 있습니다.
- 경우 1: x1 < 최빈값
표기법
| 용어 | 설명 |
|---|---|
| p1 | 첫 번째 모집단 내 사건의 실제 비율 |
| p2 | 두 번째 모집단 내 사건의 실제 비율 |
| x1 | 첫 번째 표본의 사건 수 |
| x2 | 두 번째 표본의 사건 수 |
| n1 | 첫 번째 표본의 시행 횟수 |
| n2 | 두 번째 표본의 시행 횟수 |
