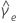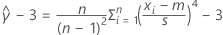원하는 방법 또는 공식을 선택하십시오.
이 항목의 내용
표준 편차
표준 편차는 산포, 즉 데이터가 평균을 중심으로 퍼져 있는 정도를 나타내는 가장 일반적인 측도입니다. 표본 표준 편차는 표본 분산의 제곱근입니다.
열에 x1, x2,..., xN이 포함되어 있고 평균이 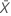 인 경우 표준 편차는 다음과 같이 계산됩니다.
인 경우 표준 편차는 다음과 같이 계산됩니다.

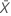 인 경우 표준 편차는 다음과 같이 계산됩니다.
인 경우 표준 편차는 다음과 같이 계산됩니다.

표기법
| 용어 | 설명 |
|---|---|
| xi | 표본의 i번째 관측치 |
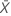 | 표본 평균 |
| S | 표본 표준 편차 |
| n | 표본 크기 |
분산
분산은 데이터가 평균 주위에 분산된 정도를 측정합니다. 분산은 표준 편차의 제곱과 같습니다.
공식
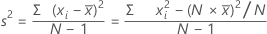
표기법
| 용어 | 설명 |
|---|---|
| xi | i번째 관측치 |
 | 관측치의 평균 |
| N | 비결측 관측치 수 |
카이-제곱 방법에 대한 신뢰 구간 및 한계
데이터가 정규 분포를 따르는 경우 이 방법을 사용합니다. 이 방법은 비정규 데이터에 대해서는 표본 크기가 아주 큰 경우에도 정확하지 않습니다.
신뢰 구간
모집단 표준 편차에 대한 100(1 - α)% 신뢰 구간은 다음과 같이 계산됩니다.
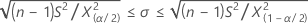
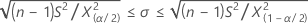
모집단 분산에 대한 100(1 - α)% 신뢰 구간은 다음과 같이 계산됩니다.


신뢰 한계
단측 검정을 지정하는 경우 Minitab에서는 대립 가설의 방향에 따라 단측 100(1–α)% 신뢰 한계를 계산합니다.
- "보다 큼" 대립 가설을 지정하는 경우 모집단 표준 편차의 100(1–α)% 하한은 다음과 같이 계산됩니다.

모집단 분산에 대한 100(1–α)% 하한은 다음과 같이 계산됩니다.
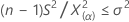
- "보다 작음" 대립 가설을 지정하는 경우 모집단 표준 편차의 100(1–α)% 상한은 다음과 같이 계산됩니다.

모집단 분산에 대한 100(1–α)% 상한은 다음과 같이 계산됩니다.

표기법
| 용어 | 설명 |
|---|---|
| α | 100(1 – α)% 신뢰 구간에 대한 알파 수준 |
| n | 표본 크기 |
| S2 | 표본 분산 |
| Χ2(p) | 자유도가 (n – 1)인 카이-제곱 분포의 상위 100p번째 백분위수 점 |
| σ | 실제 모집단 표준 편차 값 |
| σ2 | 실제 모집단 분산 값 |
Bonett 방법에 대한 신뢰 구간 및 한계
계량형 데이터(정규 또는 비정규)의 경우 이 방법을 사용합니다. 1
신뢰 구간
모집단 표준 편차에 대한 100(1-α)% 신뢰 구간은 다음과 같이 계산됩니다.


모집단 분산에 대한 100(1-α)% 신뢰 구간은 다음과 같이 계산됩니다.
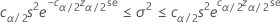
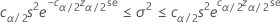
신뢰 한계
단측 검정을 지정하는 경우 Minitab에서는 대립 가설의 방향에 따라 단측 100(1–α)% 신뢰 한계를 계산합니다.
-
"보다 큼" 대립 가설을 지정하는 경우 모집단 표준 편차의 100(1–α)% 하한은 다음과 같이 계산됩니다.
 모집단 분산에 대한 근사 100(1-α)% 하한은 다음과 같이 계산됩니다.
모집단 분산에 대한 근사 100(1-α)% 하한은 다음과 같이 계산됩니다.
-
"보다 작음" 대립 가설을 지정하는 경우 모집단 표준 편차의 근사 100(1–α)% 상한은 다음과 같이 계산됩니다.
 모집단 분산에 대한 근사 100(1-α)% 상한은 다음과 같이 계산됩니다.
모집단 분산에 대한 근사 100(1-α)% 상한은 다음과 같이 계산됩니다.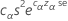
표기법
| 용어 | 설명 |
|---|---|
| α | 1 – 신뢰 수준 / 100 |
| cα/2 | n / (n – zα/2) |
| cα | n / (n – zα ) |
| s2 | 표본 분산의 관측치 |
| zα/2 | 1 – α/2에서 표준 정규 분포의 역 누적 확률. n이 zα/2보다 작거나 같은 경우 Minitab에서는 Bonett 신뢰 구간을 계산하지 않습니다. |
| zα | 1 – α에서 표준 정규 분포의 역 누적 확률. n이 zα보다 작거나 같은 경우 Minitab에서는 Bonett 신뢰 구간을 계산하지 않습니다. |
| se |  |
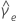 | 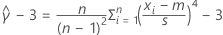 = 추정 초과 첨도 = 추정 초과 첨도 |
| m | 절사 비율이 다음과 같은 절사 평균  ; n이 5보다 작거나 같은 경우 m = 표본 평균 ; n이 5보다 작거나 같은 경우 m = 표본 평균 |
| σ | 실제 모집단 표준 편차 값 |
| σ2 | 실제 모집단 분산 값 |
카이-제곱 방법에 대한 가설 검정
데이터가 정규 분포를 따르는 경우 이 방법을 사용합니다. 이 방법은 비정규 데이터에 대해서는 표본 크기가 아주 큰 경우에도 정확하지 않습니다.
공식
가설 검정은 각 대립 가설에 대해 다음과 같은 p-값 방정식을 사용합니다.
H1: σ2 > σ02: p-값 = P(Χ2 ≥ x2)
H1: σ2 < σ02: p-값 = P(Χ2 ≤ x2)
H1: σ2 ≠ σ02: p-값 = 2 × min{P(Χ2 ≤ x2), P(Χ2 ≥ x2)}
표기법
| 용어 | 설명 | ||||||
|---|---|---|---|---|---|---|---|
| σ2 | 실제 모집단 분산 값 | ||||||
| σ02 | 귀무 가설에서의 모집단 분산 값 | ||||||
| Χ2 | σ2 = σ02일 때 자유도가 (n – 1)인 카이-제곱 분포를 따릅니다. | ||||||
| x2 | 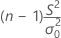
|
Bonett 방법에 대한 가설 검정
계량형 데이터(정규 또는 비정규)의 경우 이 방법을 사용합니다.
공식
Bonett 절차는 검정 통계량과 연관성이 없습니다. 그러나 Minitab에서는 신뢰 구간에 의해 정의된 기각 영역을 사용하여 p-값을 계산합니다.
양측 가설의 경우 p-값은 다음과 같이 계산됩니다.
p = 2 × min(αL, αU)
- 단측 "보다 작음" 대립 가설의 경우 p-값은 표기법에서 α/2를 α로 대치한 후 αU로 계산됩니다.
- 단측 "보다 큼" 대립 가설이 경우 p-값은 표기법에서 α/2를 α로 대치한 후 αL로 계산됩니다.
표기법
| 용어 | 설명 | ||||||
|---|---|---|---|---|---|---|---|
| σ02 | 귀무 가설에서의 분산 | ||||||
| αL | 다음 방정식의 가장 작은 해 α
 | ||||||
| αU | 다음 방정식의 가장 작은 해 α
 | ||||||
| cα/2 | n / (n – zα/2) | ||||||
| α | 1 – 신뢰 수준 / 100 | ||||||
| s2 | 표본 분산의 관측치 | ||||||
| zα/2 | 1 – α/2에서 표준 정규 분포의 역 누적 확률. n이 zα/2보다 작거나 같은 경우 Minitab에서는 Bonett 신뢰 구간을 계산하지 않습니다. | ||||||
| se | 
|
1 D.G. Bonett (2006). "Approximate confidence interval for standard deviation of nonnormal distributions" , Computational Statistics & Data Analysis, 50, 775-782.