귀무 가설과 대립 가설
- 귀무 가설
- 귀무 가설은 모집단 모수(평균, 표준 편차 등)가 귀무 가설에서의 값과 같다는 것입니다. 귀무 가설은 종종 이전 분석 또는 전문 지식을 기반으로 한 초기 주장입니다.
- 대립 가설
- 대립 가설은 모집단 모수가 귀무 가설에서의 값보다 작거나 크거나 다르다는 것입니다. 대립 가설은 검정 당사자가 참이라고 믿거나 참으로 증명되기를 바라는 것입니다.
해석
결과에서 귀무 가설과 대립 가설은 귀무 가설에서의 표준 편차 또는 분산에 대해 올바른 값을 입력했는지 확인하는 데 도움이 됩니다.
N
표본 크기(N)는 표본의 총 관측치 수입니다.
해석
표본 크기는 신뢰 구간 및 검정의 검정력에 영향을 미칩니다.
일반적으로 표본 크기가 클수록 신뢰 구간이 좁아집니다. 또한 표본 크기가 클수록 차이를 탐지하기 위한 검정력이 더 높습니다. 자세한 내용은 검정력의 정의에서 확인하십시오.
표준 편차
표준 편차는 산포, 즉 데이터가 평균을 중심으로 퍼져 있는 정도를 나타내는 가장 일반적인 측도입니다. 모집단의 표준 편차를 나타내는 데는 σ(시그마) 기호를 자주 사용하는 반면, 표본의 표준 편차를 사용하는 데는 s를 사용합니다. 랜덤이 아니거나 공정에 자연스럽지 못한 변동은 종종 잡음이라고 합니다.
표준 편차는 데이터와 동일한 단위를 사용합니다.
해석
표본 데이터의 표준 편차는 모집단 표준 편차의 추정치입니다.
표준 편차는 전체 모집단이 아니라 표본 데이터를 기반으로 하기 때문에 표본 표준 편차가 모집단 표준 편차와 같을 가능성은 없습니다. 모집단 표준 편차를 더 잘 추정하려면 신뢰 구간을 사용하십시오.
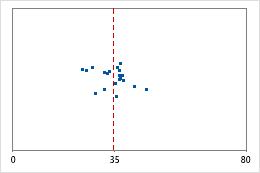
병원 1
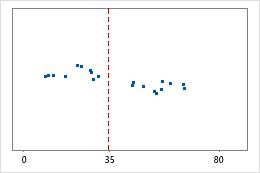
병원 2
병원 퇴원 시간
관리자들이 두 개 병원의 응급실 부서에서 치료한 환자의 퇴원 시간을 추적하고자 합니다. 평균 퇴원 시간은 동일하지만(35분) 표준 편차는 유의하게 다릅니다. 병원 1의 표준 편차가 약 6이며, 평균적으로 환자의 퇴원 시간은 평균(대시선)에서 약 6분 정도 멀어집니다. 병원 2의 표준 편차는 약 20입니다. 평균적으로 환자의 퇴원 시간은 평균(대시선)에서 약 20분 정도 멀어집니다.
분산
분산은 데이터가 평균 주위에 분산된 정도를 측정합니다. 분산은 표준 편차의 제곱과 같습니다.
해석
표본 데이터의 분산은 모집단 분산의 추정치입니다.
분산은 전체 모집단이 아니라 표본 데이터를 기반으로 하기 때문에 표본 분산이 모집단 분산과 같을 가능성은 없습니다. 모집단 분산을 더 잘 추정하려면 신뢰 구간을 사용하십시오.
신뢰 구간(CI) 및 한계
신뢰 구간은 모집단 표준 편차 또는 모집단 분산이 될 수 있는 값의 범위를 제공합니다. 표본이 랜덤이기 때문에 모집단의 두 표본에서 동일한 신뢰 구간이 생성될 가능성은 없습니다. 그러나 표본 추출을 여러 번 반복하면 일정한 백분율의 신뢰 구간이나 한계에는 알 수 없는 모집단 표준 편차 또는 모집단 분산이 포함됩니다. 표준 편차 또는 모집단 분산을 포함하는 이러한 신뢰 구간 또는 한계의 백분율이 해당 구간의 신뢰 수준입니다. 예를 들어, 95% 신뢰 수준은 모집단에서 100개의 랜덤 표본을 추출할 경우 약 95개의 표본에서 모집단 표준 편차 또는 모집단 분산이 포함된 구간을 생성할 것으로 예상된다는 것을 나타냅니다.
상한은 모집단 표준 편차나 모집단 분산이 더 작을 가능성이 높은 값을 정의합니다. 하한은 모집단 표준 편차나 모집단 분산이 더 클 가능성이 높은 값을 정의합니다.
신뢰 구간은 결과의 실제 유의성을 평가하는 데 도움이 됩니다. 해당 상황에 실제적으로 유의한 값이 신뢰 구간에 포함되는지 여부를 확인하려면 전문 지식을 이용하십시오. 신뢰 구간이 너무 넓어서 유의하지 않은 경우에는 표본 크기를 늘려보십시오. 자세한 내용은 더 정밀한 신뢰 구간을 구하는 방법에서 확인하십시오.
참고
데이터 열을 입력하면 Minitab에서는 표준 편차에 대한 신뢰 구간만 계산합니다.
참고
요약 데이터로 Bonett 방법을 계산할 수 없습니다.
기술 통계량
| N | 표준 편차 | 분산 | Bonett을 사용한 σ에 대 한 95% CI | 카이-제곱을 사용한 σ에 대한 95% CI |
|---|---|---|---|---|
| 50 | 0.871 | 0.759 | (0.704, 1.121) | (0.728, 1.085) |
이 결과에서 빔 길이에 대한 모집단 표준 편차의 추정치는 0.871이고 모집단 분산의 추정치는 0.759입니다. 데이터가 정규성 검정을 통과하지 못했으므로 Bonett 방법을 사용하십시오. 모집단 표준 편차가 0.704와 1.121 사이에 있다고 95% 확신할 수 있습니다.
검정 통계량
관측된 분산과 귀무 가설에서의 분산의 비율을 측정하는 카이-제곱 검정을 위한 검정 통계량입니다.
해석
검정 통계량을 카이-제곱 분포의 임계값과 비교하여 귀무 가설의 기각 여부를 확인할 수 있습니다. 그러나 일반적으로 검정의 p-값을 사용하여 결정을 내리는 것이 더 실제적이고 편리합니다. 검정 크기에 관계없이 p-값은 동일한 의미를 갖지만, 표본 크기에 따라 동일한 카이-제곱 통계량이 반대의 결론을 나타낼 수 있습니다.
- 양측 검정의 경우 임계값은
및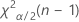 
입니다. 검정 통계량이 첫 번째 값보다 작거나 두 번째 값보다 크면 귀무 가설을 기각합니다. 첫 번째 값과 두 번째 값 사이에 있으면 귀무 가설을 기각할 수 없습니다. - 보다 작음 대립 가설의 단측 검정의 경우 임계값은
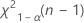입니다. 검정 통계량이 이 값보다 작으면 귀무 가설을 기각합니다. 그렇지 않으면 귀무 가설을 기각할 수 없습니다. - 보다 큼 단측 검정의 경우 임계값은
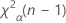입니다. 검정 통계량이 이 값보다 크면 귀무 가설을 기각합니다. 그렇지 않으면 귀무 가설을 기각할 수 없습니다.
검정 통계량은 p-값을 계산하기 위해 사용됩니다. Bonnet 방법에 대한 검정 통계량이 없기 때문에 Minitab에서는 신뢰 구간에 의해 정의된 기각 영역을 사용하여 p-값을 계산합니다.
DF
자유도(DF)는 데이터에서 알 수 없는 모수를 추정하고 이러한 추정치의 변동성을 계산하는 데 사용할 수 있는 정보의 양을 나타냅니다. 단일 표본 분산의 경우, 자유도는 표본의 관측치 수에 따라 결정됩니다.
해석
Minitab에서는 검정 통계량을 계산하기 위해 자유도를 사용합니다. 자유도는 표본 크기에 따라 결정됩니다. 표본 크기를 증가시키면 모집단에 대한 더 많은 정보가 제공되므로, 자유도가 증가합니다.
p-값
p-값은 귀무 가설에 반하는 증거를 측정하는 확률입니다. p-값이 작을수록 귀무 가설에 반하는 더 강력한 증거가 됩니다.
해석
모집단 분산 또는 표준 편차가 귀무 가설에서의 분산 또는 표준 편차와 통계적으로 다른지 여부를 확인하려면 p-값을 사용하십시오.
- p-값 ≤ α: 분산 또는 표준 편차 간의 차이가 통계적으로 유의함(H0 기각)
- p-값이 유의 수준보다 작거나 같으면 귀무 가설을 기각합니다. 모집단 분산 또는 표준 편차와 귀무 가설에서의 분산 또는 표준 편차 간의 차이가 통계적으로 유의하다는 결론을 내릴 수 있습니다. 차이가 실제로 유의한지 여부를 확인하려면 전문 지식을 활용합니다. 자세한 내용은 통계적 유의성 및 실제적 유의성에서 확인하십시오.
- p-값 > α: 분산 또는 표준 편차 간의 차이가 통계적으로 유의하지 않음(H0 기각 실패)
- p-값이 유의 수준보다 크면 귀무 가설을 기각할 수 없습니다. 모집단 분산 또는 표준 편차와 귀무 가설에서의 분산 또는 표준 편차 간의 차이가 통계적으로 유의하다는 결론을 내릴 충분한 증거가 없습니다.검정에 실제로 유의한 차이를 탐지할 만한 충분한 검정력이 있는지 확인해야 합니다. 자세한 내용은 단일 표본 분산에 대한 검정력 및 표본 크기에서 확인하십시오.
참고
요약 데이터가 있는 경우 Minitab에서 Bonett 방법에 대한 p-값을 계산할 수 없습니다.
