통계량
| 용어 | 설명 |
|---|---|
| 발생률 |
 |
| 평균 발생 횟수 |
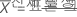 |
비율은 관측치의 단위 길이당 평균 발생 횟수와 같습니다. 평균은 전체 표본의 평균 발생 횟수입니다. 길이가 1인 경우 비율과 평균이 같습니다.
정확 검정에 대한 p-값
공식
- H1: λ > λ0: p-값 = P(S ≥ s | λ = λ0), 여기서 S는 평균이 nλ0t인 포아송 분포를 따릅니다.
- H1: λ < λ0: p-값 = P(S ≤ s | λ = λ0), 여기서 S는 평균이 nλ0t인 포아송 분포를 따릅니다.
- H1: λ ≠ λ0: Minitab에서 다음과 같은 우도 비 검정을 사용합니다.
포아송 공정의 전체 발생 횟수, s의 관점에서 우도 비 검정을 표현하는 함수 G(s)를 정의합니다.

- 0 ≤ s < nλ0t인 경우 구간 (nλ0t, enλ0t]에서 y에 대한 방정식 G(y) = G(s)의 해를 구합니다.
p-값 = P(S ≤ s | λ = λ0) + P(S ≥ y | λ = λ0)
- s = nλ0t인 경우
p-값 = 1.00
- nλ0t < s ≤ enλ0t인 경우 구간 [0, nλ0t)에서 y에 대한 방정식 G(y) = G(s)의 해를 구합니다.
p-값 = P(S ≤ y | λ = λ0) + P(S ≥ s | λ = λ0)
- s > enλ0t인 경우 검정은 단측이며
p-값 = P(S ≥ s | λ = λ0)입니다.
여기서 S는 평균이 nλ0t인 포아송 분포를 따릅니다.
- 0 ≤ s < nλ0t인 경우 구간 (nλ0t, enλ0t]에서 y에 대한 방정식 G(y) = G(s)의 해를 구합니다.
표기법
| 용어 | 설명 |
|---|---|
| s | 포아송 공정의 전체 발생 횟수 |
| t | 관측치의 "길이" |
| λ0 | 모집단 비율 모수의 귀무 가설에서의 값 |
| λ | 모집단 비율 모수의 실제 값 |
| n | 표본 크기 |
| e | 약 2.71828 |
정확 검정에 대한 신뢰 구간 및 신뢰 한계
신뢰 구간
포아송 공정의 발생률에 대한 정확한 100(1 – α)% 신뢰 구간은 다음과 같이 계산됩니다.
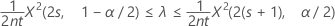
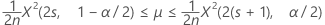
신뢰 한계
단측 검정을 지정하는 경우 Minitab에서는 대립 가설의 방향에 따라 단측 100(1 – α)% 신뢰 한계를 계산합니다.
-
"보다 큼" 대립 가설을 지정하는 경우 비율의 정확한 100(1 – α)% 신뢰 하한은 다음과 같이 계산됩니다.
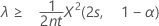
평균의 정확한 100(1 – α)% 신뢰 하한은 다음과 같이 계산됩니다.
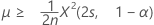
-
"보다 작음" 대립 가설을 지정하는 경우 비율의 정확한 100(1 – α)% 신뢰 상한은 다음과 같이 계산됩니다.
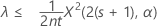
평균의 정확한 100(1 – α)% 신뢰 상한은 다음과 같이 계산됩니다.
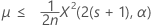
표기법
| 용어 | 설명 |
|---|---|
| s | 포아송 공정의 전체 발생 횟수 |
| t | 관측치의 "길이" |
| λ | 모집단 비율의 실제 값 |
| μ | 모집단 평균의 실제 값 |
| Χ2(p, x) | 자유도가 p인 Χ2 분포의 상위 x 백분위수 점, 여기서 0 < x < 1. |
| α | 100(1 – α)% 신뢰 구간에 대한 알파 수준 |
| n | 표본 크기 |
정규 근사에 대한 p-값
전체 발생 횟수가 10보다 큰 경우 정규 근사가 유효합니다.
공식
1-표본 포아송 비율에 대한 정규 근사에 기초한 가설 검정은 각 대립 가설에 대해 다음과 같은 p-값 방정식을 사용합니다.


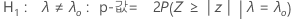
표기법
| 용어 | 설명 |
|---|---|
| Z | 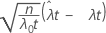 |
| t | 관측치의 "길이" |
| λ 0 | 모집단 비율 모수의 귀무 가설에서의 값 |
| λ | 모집단 비율 모수의 실제 값 |
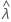 | 표본 비율 통계량의 관측치 |
| n | 표본 크기 |
정규 근사에 대한 신뢰 구간 및 신뢰 한계
신뢰 구간
정규 근사에 기초한 포아송 공정의 발생률에 대한 100(1 – α)% 신뢰 구간은 다음과 같이 계산됩니다.
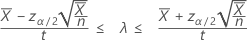
"길이" 값을 지정하는 경우 Minitab에서는 평균 발생 횟수에 대한 신뢰 구간도 표시합니다. 이 신뢰 구간은 다음과 같이 계산됩니다.
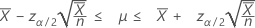
신뢰 한계
단측 검정을 지정하는 경우 Minitab에서는 대립 가설의 방향에 따라 단측 100(1 – α)% 신뢰 한계를 계산합니다.-
"보다 큼" 대립 가설을 지정하는 경우 비율의 정확한 100(1 – α)% 신뢰 하한은 다음과 같이 계산됩니다.
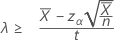
"길이" 값을 지정하는 경우 평균의 정확한 100(1-α)% 신뢰 하한은 다음과 같이 계산됩니다.
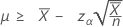
-
"보다 작음" 대립 가설을 지정하는 경우 비율의 정확한 100(1 – α)% 신뢰 상한은 다음과 같이 계산됩니다.
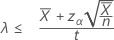
"길이" 값을 지정하는 경우 평균의 정확한 100(1 – α)% 신뢰 상한은 다음과 같이 계산됩니다.
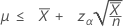
표기법
| 용어 | 설명 |
|---|---|
| s | 포아송 공정의 전체 발생 횟수 |
| t | 관측치의 "길이" |
| λ | 모집단 비율의 실제 값 |
| μ | 모집단 평균의 실제 값 |
| Zx | 표준 정규 분포의 상위 x 백분위수 점, 여기서 0 < x < 1. |
| α | 100(1 – α)% 신뢰 구간에 대한 알파 수준 |
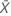 | 표본의 평균 발생 횟수 |
| n | 표본 크기 |
