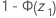이 항목의 내용
수정된 Blaker 정확한 신뢰 구간 및 검정 방법
수정된 Blaker 정확 방법은 사건 비율에 대한 양측 신뢰 구간을 생성하고 p ≠ p0의 대립 가설에 대한 p -값을 생성합니다. Blaker12 는 정확 검정의 p-값 함수를 반전하여 정확한 양측 신뢰 구간을 제공합니다. Clopper-Pearson 구간은 더 넓으며 항상 Blaker 신뢰 구간을 포함합니다. Blaker 정확 방법의 구간은 내포되어 있습니다. 이 속성은 신뢰 수준이 높은 신뢰 구간에 신뢰 수준이 낮은 신뢰 구간이 포함된다는 것을 의미합니다. 예를 들어, 정확한 양측 Blaker 95% 신뢰 구간에는 해당하는 90% 신뢰 구간이 포함됩니다.
Blaker의 원래 정확한 방법에는 2가지 제한 사항이 있습니다. 한 가지 제한 사항은 신뢰 구간을 계산하는 수치 알고리즘이 느리다는 점이며, 특히 표본 크기가 클 때는 더욱 그렇습니다. 또 다른 제한 사항은 일부 데이터의 경우 원래 Blaker 정확 방법이 p-값이 신뢰 수준에 해당하는 유의 수준보다 작을 때 귀무 가설에서의 비율을 포함하는 구간을 생성한다는 것입니다. 또한 신뢰 구간에 귀무 가설에서의 비율이 포함되지 않은 경우에도 p-값이 신뢰 수준에 해당하는 유의 수준보다 큽니다.
이러한 한계를 극복하기 위해 Minitab Statistical Software의 분석에서는 Klaschka 및 Reiczigel의 알고리즘을 사용하여 신뢰 구간과 p-값을 생성합니다.3 이 방법의 이름은 수정된 Blaker 정확 방법입니다. 이 수치 알고리즘은 계산 속도가 더 빠르며 일반적으로 일치하는 신뢰 구간과 검정을 생성합니다. 수정된 Blaker 신뢰 구간도 정확하며 내포되어 있습니다.
보다 작거나 큰 대립 가설의 경우 분석에서는 Clopper-Pearson 정확 방법을 사용합니다.
Clopper-Pearson 정확한 신뢰 구간 방법
구간 (PL, PU)는 p의 양측 100(1 – α)% 신뢰 구간입니다. 표본에 사건이 없는 경우 하한은 0입니다. 표본에 사건만 있는 경우 상한은 1입니다.
하한
수식
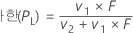
표기법
| 용어 | 설명 |
|---|---|
| v1 | 2x |
| v2 | 2(n – x + 1) |
| x | 사건 발생 횟수 |
| n | 시행 횟수 |
| F | 자유도가 v1 및 v2인 F 분포의 하위 α/2 점 |
상한
수식
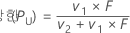
표기법
| 용어 | 설명 |
|---|---|
| v1 | 2(x + 1) |
| v2 | 2(n – x) |
| x | 사건 발생 횟수 |
| n | 시행 횟수 |
| F | 자유도가 v1 및 v2인 F 분포의 상위 α/2 점 |
Clopper-Pearson 정확 신뢰 구간에 해당하는 검정
수식
- Hi: p ≠ p0
- p-값 =
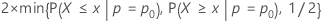
- Hi: p > p0
- p-값 = P{ X ≥ x | p = po}
- Hi: p < p0
- p-값 = P{ X ≤ x | p = po}
표기법
| 용어 | 설명 |
|---|---|
| p0 | 귀무 가설에서의 비율 |
| n | 시행 횟수 |
| p | 사건 확률 |
| x | 사건 발생 횟수 |
Wilson-score 신뢰 구간 방법
윌슨4 Minitab Statistical Software에서 Wilson-score 신뢰 구간으로 명명한 신뢰 구간을 얻기 위해 점수 검정을 반전합니다. 윌슨 점수 구간에는 연속성 수정이 없는 형식과 연속성 수정이 있는 형식의 두 가지 형식이 있습니다. 수정이 없는 구간의 범위가 명목 신뢰 수준보다 낮은 경우가 있습니다. 수정이 있는 구간의 실제 신뢰 수준은 적어도 명목 신뢰 수준입니다. 두 방법 모두 표본에 사건이 없는 경우 하한은 0입니다. 표본에 사건만 있는 경우 상한은 1입니다.
연속성 보정이 없는 간격
양측 100(1 – α)% 신뢰 구간의 공식은 다음과 같습니다.
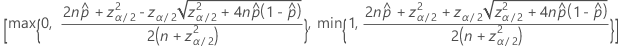
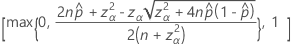
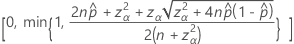
연속성 보정이 있는 간격
양측 100(1 – α)% 구간의 하한은 다음과 같은 공식을 갖습니다.
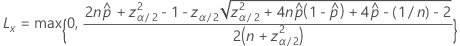
양측 100(1 – α)% 구간의 상한은 다음과 같은 공식을 갖습니다.
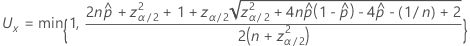
단측 100(1 – α)% 하한의 공식은 다음과 같습니다.
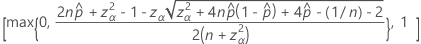
단측 100(1 – α)% 상한의 공식은 다음과 같습니다.
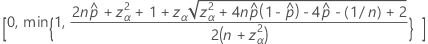
표기법
| 용어 | 설명 |
|---|---|
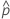 | 관측된 확률, 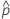 = x / n = x / n |
| x | 사건 발생 횟수 |
| n | 시행 횟수 |
| zγ | γ에서 표준 정규 분포의 상위 백분위수 점 |
| α | 1 – 신뢰 수준/100 |
점수 테스트
연속성 보정이 없는 방법
Wilson-score 신뢰 구간 및 정규 근사 방법(웹 앱)에 해당하는 테스트는 잘 알려진 점수 테스트입니다. 점수 검정 통계량에는 다음과 같은 수식이 있습니다.
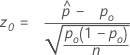
- Ha: p ≠ p0
- p-값 =
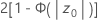
- Ha: p > p0
- p-값 =

- Ha: p < p0
- p-값 =

연속성 보정이 있는 방법
연속성 수정이 있는 절차에 대한 검정 통계량과 p-값은 대립 가설에 따라 달라집니다.
- Ha: p ≠ p0
-
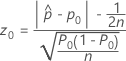
- Ha: p > p0
-
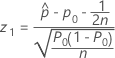
- Ha: p < p0
-
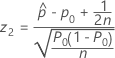
표기법
| 용어 | 설명 |
|---|---|
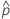 | 관측된 확률 x/n |
| x | 사건 발생 횟수 |
| n | 시행 횟수 |
| p0 | 귀무 가설에서의 비율 |
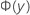 | y에서의 표준 정규 분포의 누적 분포 함수 |
Agresti-Coull 신뢰 구간 및 검정 방법
신뢰 구간
Agresti와 Coull5 은 커버리지 속성을 개선하는 신뢰 구간에 대한 Wald 방법에 대한 조정을 제공합니다. 양측 95% 신뢰 구간의 경우 조정은 약 2개의 사건과 2개의 비사건을 추가한 다음 Wald 신뢰 구간 공식에 대한 공식에서 신뢰 구간을 계산합니다. 표본에 사건이 없는 경우 하한은 0입니다. 표본에 사건만 있는 경우 상한은 1입니다.
양측 100(1 – α)% 구간의 공식은 다음과 같습니다.
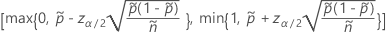
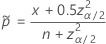
및
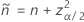
단측 100(1 – α)% 하한의 공식은 다음과 같습니다.
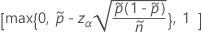
단측 100(1 – α)% 상한의 공식은 다음과 같습니다.
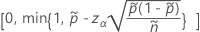
단측 한계의 경우  의 정의에서
의 정의에서 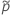 및
및 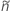 :
:
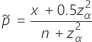
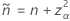
Agresti-Coull 구간에 해당하는 검정
분석에서는 신뢰 구간 절차를 반전하여 검정에 대한 p-값을 계산합니다.
표기법
| 용어 | 설명 |
|---|---|
| x | 사건 발생 횟수 |
| n | 시행 횟수 |
| zγ | γ에서 표준 정규 분포의 상위 백분위수 점 |
| α | 1 – 신뢰 수준/100 |
Wald 정규 근사에 대한 신뢰 구간(웹앱)
수식
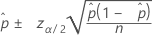
표기법
| 용어 | 설명 |
|---|---|
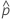 | 관측된 확률, 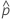 = x / n = x / n |
| x | n번의 시행에서 관측된 사건 수 |
| n | 시행 횟수 |
| zα/2 | 1 – α/2에서 표준 정규 분포의 역 누적 확률. |
| α | 1 – 신뢰 수준/100 |