개별 및 종합 만족도는 입력 변수의 조합이 반응 변수에 대해 정의한 목표를 만족하는 정도를 평가합니다. 개별 만족도(d)는 해당 설정이 단일 반응 변수를 최적화하는 정도를 평가합니다. 종합 만족도(D)는 해당 설정이 여러 반응 변수를 전체적으로 최적화하는 정도를 평가합니다. 만족도의 범위는 0에서 1까지입니다. 1은 이상적인 경우를 나타내고, 0은 하나 이상의 반응이 허용 한계를 벗어난다는 것을 나타냅니다.
예를 들어, 한 화학 제품 엔지니어가 반응 시간, 반응 온도, 촉매 유형 등 세 변수에 변화를 주어 화학 반응의 수율을 극대화하려고 합니다. 이와 동시에 비용도 최소화하려고 하는 데, 비용도 세 가지 변수의 영향을 받습니다. 엔지니어는 반응 최적화 도구를 사용하여 목표 수율과 목표 비용을 정의할 수 있습니다. Minitab은 만족도 값과 함께 만족도 변수의 최적 설정을 계산하고 각 설정에서 반응 변수의 목표값을 달성하는 정도를 표시합니다.
여기서 종합 만족도(0.9245)는 1에 가까우며, 이는 해당 설정이 모든 반응 변수에 대해 전체적으로 만족스러운 결과를 낸다는 것을 의미합니다. 그러나 개별 만족도는 해당 설정이 비용을 최소화(0.87136)하는 것보다 수율을 최대화(0.98077)하는 데 더욱 효과적임을 나타냅니다. 비용을 최소화하는 것이 더 중요하면 최적화 그림을 사용하여 비용의 개별 만족도를 높이고 수율의 개별 만족도는 낮추도록 설정을 조정할 수 있습니다.
Minitab의 반응 최적화 도구는 만족도 함수(효용 전이 함수라고도 함)를 사용하여 개별 만족도를 계산합니다. 가중치(0.1 - 10)를 선택하여 해당 반응 변수의 목표값 달성이 얼마나 중요한지 지정할 수 있습니다. 종합 만족도는 반응에 대한 개별 만족도의 가중 기하 평균입니다. 종합 만족도를 최적화하여 변수의 최적 설정을 결정합니다.
모수의 조합이 만족도 함수를 생성하는 예
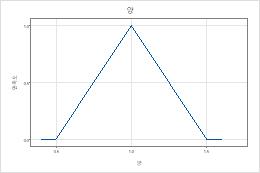
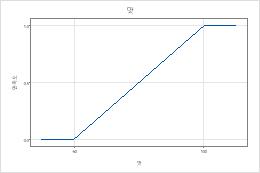
다음 그래프는 퐁듀 데이터 반응 맛과 양에 대한 모수 조합으로 만족도 함수를 생성하는 방법을 보여줍니다.
| 목적 | 하한점 | 목표값 | 상한점 | 가중치 | 중요도 |
|---|---|---|---|---|---|
| 최대값 | 60 | 100 | 100 | 1 | 2 |
| 목적 | 하한점 | 목표값 | 상한점 | 가중치 | 중요도 |
|---|---|---|---|---|---|
| 최대값 | 0.5 | 1 | 1.5 | 1 | 1 |