이 항목의 내용
다중 쌍 비교를 위한 그룹화 정보 표
Minitab에서는 두 수준 평균 간의 차이에 대한 신뢰 구간 결과를 사용하여 그룹화 정보를 얻습니다. 그룹화 정보는 행렬에 포함되어 있습니다. 한 항에 k개의 수준이 있고 행렬의 최대 크기가 k x k라고 가정합니다. 모든 수준이 한 그룹에 있는 경우 크기는 k x 1이고, 문자 "A"는 모든 요인 수준을 나타냅니다. 모든 수준이 서로 다른 그룹에 있는 경우에는 크기가 k x k이고 대각선에만 문자가 표시됩니다.
- 항의 여러 수준에서 모든 최소 제곱 평균을 내림차순으로 정렬하고 1, 2, ... , k로 표시합니다.
- k x k 행렬을 정의하고 모든 셀에 0을 입력합니다. 여기서 k = 요인 수준의 수입니다.
- 열 j(j = 1, ...)에 대해 Minitab에서는 다음을 수행합니다.
- 평균 j – 평균 r(r = j + 1, .. , k)의 신뢰 구간을 확인합니다. r에 대한 구간에 0이 포함되어 있으면 r번째 행과 j번째 열 셀 (r, j)를 1로 설정합니다.
- 열 j에 있는 하나 이상의 셀의 값이 1인 경우 (j, j) 셀을 1로 설정합니다.
- 행 I = j + 1, ... , k에 대해 열 1에서 열 j까지 행 합을 계산합니다. min(모든 행 합) >= 1이면 루프를 종료하고, 그렇지 않으면 j를 1 증가시켜 단계 a로 이동합니다.
- 모든 행 i에 대해 Minitab에서는 1 이상의 모든 행에 대해 모든 열 값의 합을 확인합니다. 합이 0이면 행 i와 열 j의 셀을 1로 설정합니다. 여기서 j는 행렬에서 값이 0인 첫 번째 열입니다. 이 절차를 실행하면 값이 1과 0인 행렬이 생성됩니다. 총 그룹 수는 0이 아닌 열의 수입니다.
- Minitab에서는 A와 열 1, B와 열 2 등과 같이 문자를 열과 일치시키고 값이 1인 열에 올바른 문자를 할당합니다.
관리 수준에서의 다중 비교를 위한 그룹화 정보 표
Minitab에서는 각 수준 평균과 관리 수준 간의 차이에 대한 신뢰 구간 결과를 사용하여 그룹화 정보를 얻습니다. 그룹화 정보는 단일 열이 있는 행렬에 포함되어 있습니다.
Minitab에서는 문자 "A"를 관리 수준에 할당합니다.
구간에 0이 포함되어 있으면 수준 평균이 관리 수준과 같은 그룹에 있습니다. Minitab에서는 문자 "A"를 수준 평균에 할당합니다.
구간에 0이 포함되어 있지 않으면 문자가 할당되지 않습니다.
Tukey의 방법
공식
Tukey의 방법은 모든 쌍별 비교에 사용할 수 있습니다. 신뢰 구간에 대한 공식은 다음과 같습니다.
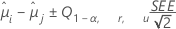
검정 통계량에 대한 공식은 다음과 같습니다.

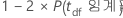
수정된 p-값 계산에 대한 자세한 내용은 아래의 참고 문헌을 참조하십시오.
동시 오류율에서 개별 오류율을 찾으려면 다음 공식을 사용하십시오.
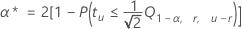
표기법
| 용어 | 설명 |
|---|---|
 | i번째 요인 수준 또는 요인 수준 조합에 대한 최소 제곱 평균 |
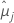 | j번째 요인 수준 또는 요인 수준 조합에 대한 최소 제곱 평균 |
| r | 평균 수 |
| Q1 − α, r, u | 비교할 r개의 평균에 대한 자유도가 u인 스튜던트화된 범위 분포의 1 − α 백분위수 |
| u | 모형의 오차에 대한 자유도 |
| SEE | 최소 제곱 평균 간 추정된 차이의 표준 오차 |
| α | 스튜던트화된 범위 분포를 기반으로 한, 제1종 오류를 범할 동시 확률 |
| α* | 하나의 비교에 대한 t-분포를 기반으로 한, 제1종 오류를 범할 개별 확률 |
참고 문헌
1 Braun, H. I., editor (1994). The collected works of John W. Tukey: Volume VIII Multiple comparisons 1948-1983. New York: Chapman and Hall.
2 J.C. Hsu (1996). Multiple Comparisons: Theory and methods. Chapman & Hall.
Fisher 방법
공식
Minitab에서는 처리 평균을 비교하기 위한 여러 가지 신뢰 구간 방법을 제공합니다. Fisher 방법의 경우, 신뢰 구간 끝 점과 p-값은 비교가 쌍 비교이거나 관리 수준에서의 비교이거나 관계없이 같습니다. Fisher 방법은 개별 신뢰 수준을 사용합니다. 신뢰 구간에 대한 공식은 다음과 같습니다.
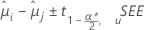
검정 통계량에 대한 공식은 다음과 같습니다.

p-값 = 2*P{ T u > tu}
개별 오류율에서 동시 신뢰 수준을 찾으려면 다음 공식을 사용하십시오.
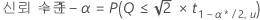
표기법
| 용어 | 설명 |
|---|---|
 | i번째 요인 수준 또는 요인 수준 조합에 대한 최소 제곱 평균 |
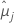 | j번째 요인 수준 또는 요인 수준 조합에 대한 최소 제곱 평균 |
| t1-α*/2, u | 자유도가 u인 스튜던트의 t-분포의 상위 α*/2 백분위수 |
| Tu | 오차에 대한 자유도가 u인 T 분포를 따르는 랜덤 변수 |
| Q | 스튜던트화된 범위 분포를 따르는 랜덤 변수 |
| α | 제1종 오류를 범할 동시 확률 |
| α* | 제1종 오류를 범할 개별 확률 |
| u | 모형의 오차에 대한 자유도 |
| SEE | 최소 제곱 평균 간 추정된 차이의 표준 오차 |
Bonferroni의 방법
공식
Minitab에서는 처리 평균을 비교하기 위한 여러 가지 신뢰 구간 방법을 제공합니다. Bonferroni 방법은 비교 간의 종속성에 대한 가정을 하지 않기 때문에 가장 보수적인 방법입니다. 여기서 "보수적"이라는 것은 실제 신뢰 수준이 표시되는 신뢰 수준보다 클 가능성이 있다는 것을 나타냅니다. 신뢰 구간에 대한 공식은 다음과 같습니다.
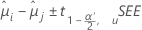
검정 통계량에 대한 공식은 다음과 같습니다.

표기법
| 용어 | 설명 |
|---|---|
 | i번째 요인 수준 또는 요인 수준 조합에 대한 최소 제곱 평균 |
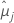 | j번째 요인 수준 또는 요인 수준 조합에 대한 최소 제곱 평균 |
| t1-α*/2, u | 자유도가 u인 스튜던트의 t-분포의 상위 α' /2 백분위수 |
| α | 제1종 오류를 범할 동시 확률 |
| α' | α / c |
| c | 비교의 수 |
| u | 모형의 오차에 대한 자유도 |
| SEE | 최소 제곱 평균 간 추정된 차이의 표준 오차 |
비교의 수는 비교가 쌍 비교인지 또는 관리 수준에서의 비교인지 여부에 따라 다릅니다. k를 비교 중인 평균의 수로 설정합니다. 비교의 수는 아래 표에 있습니다.
| 쌍별 비교 | k (k – 1) / 2 |
| 관리 수준에서의 비교 | k – 1 |
Sidak의 방법
공식
Minitab에서는 처리 평균을 비교하기 위한 여러 가지 신뢰 구간 방법을 제공합니다. Sidak 방법은 비교를 서로 독립적인 것처럼 처리하므로, 실제 오류율의 보수적인 근사치가 생성됩니다. Sidak 방법은 Bonferroni 방법보다 약간 더 강력합니다.
신뢰 구간에 대한 공식은 다음과 같습니다.
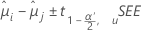
검정 통계량에 대한 공식은 다음과 같습니다.

수정된 p-값 = 1 − (1 − p)c.
표기법
| 용어 | 설명 |
|---|---|
 | i번째 요인 수준 또는 요인 수준 조합에 대한 최소 제곱 평균 |
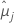 | j번째 요인 수준 또는 요인 수준 조합에 대한 최소 제곱 평균 |
| t1-α*/2, u | 자유도가 u인 스튜던트의 t-분포의 상위 α' /2 백분위수 |
| α | 제1종 오류를 범할 동시 확률 |
| α' | 1 – (1 – α ) 1/ k |
| u | 모형의 오차에 대한 자유도 |
| SEE | 최소 제곱 평균 간 추정된 차이의 표준 오차 |
| p | 비교에 대한 t-분포의 수정되지 않은 p-값 |
| c | 비교의 수 |
비교의 수는 비교가 쌍 비교인지 또는 관리 수준에서의 비교인지 여부에 따라 다릅니다. k를 요인 조합의 수로 설정합니다. 비교의 수는 아래 표에 있습니다.
| 쌍별 비교 | k (k – 1) / 2 |
| 관리 수준에서의 비교 | k – 1 |
Dunnett의 방법
공식
Minitab에서는 처리 평균을 비교하기 위한 여러 가지 신뢰 구간 방법을 제공합니다. Dunnet의 방법은 관리 수준에서의 비교에 사용할 수 있습니다. 신뢰 구간에 대한 공식은 다음과 같습니다.

검정 통계량에 대한 공식은 다음과 같습니다.

수정된 p-값은 Dunnett이 제안하는 검정 통계량의 분포를 통합한 결과입니다. 자세한 내용은 아래의 참고 문헌을 참조하십시오.
표기법
| 용어 | 설명 |
|---|---|
 | i번째 요인 수준 또는 요인 수준 조합에 대한 최소 제곱 평균 |
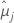 | j번째 요인 수준 또는 요인 수준 조합에 대한 최소 제곱 평균 |
| D1-α, k-1, u | Dunnett이 제안하는 비교가 k - 1이고 자유도가 u인 분포의 상위 α 백분위수 |
| α | 제1종 오류를 범할 동시 확률 |
| k | 비교할 평균 수 |
| u | 모형의 오차에 대한 자유도 |
| SEE | 최소 제곱 평균 간 추정된 차이의 표준 오차 |
참고 문헌
1 Dunnett, C. W. (January 01, 1955). A multiple comparison procedure for comparing several treatments with a control. Journal of the American Statistical Association, 50, 1096-1121.
2 J.C. Hsu (1996). Multiple Comparisons: Theory and methods. Chapman & Hall.
