원하는 방법 또는 공식을 선택하십시오.
선형
공식
선형 추세 모형은 다음과 같습니다.
Yt = β0 + β1t + et
표기법
| 용어 | 설명 |
|---|---|
| β0 | 상수 |
| β1 | 한 기간부터 다음 기간까지의 평균 변화 |
| t | 시간 단위의 값 |
| et | 오차항 |
지수 성장
공식
지수 성장 추세 모형은 지수 성장 및 감소를 설명합니다. 예를 들어, 예금액은 지수 성장을 나타냅니다.
Yt = β0 * β1t * et
표기법
| 용어 | 설명 |
|---|---|
| β0 | 상수 |
| β1 | 계수 |
| t 분포 | 시간 단위의 값 |
| et | 오차항 |
2차
공식
2차 추세 모형은 데이터의 단순 곡면성을 설명할 수 있습니다. 이 모형은 다음과 같습니다.
Yt = β0 + β1t + β2t2 + et
표기법
| 용어 | 설명 |
|---|---|
| β0 | 상수 |
| β1 및 β2 | 계수 |
| t | 시간 단위의 값 |
| et | 오차항 |
S-곡선
공식
데이터에는 S-형이 있어 변화 방향이 시간이 지남에 따라 달라진다는 것을 나타냅니다.
Yt = 10a / (β0 + β1β2t)
표기법
| 용어 | 설명 |
|---|---|
| β0 | 상수 |
| β1 및 β2 | 계수 |
| t | 시간 단위의 값 |
가중치
이전 추세 분석 적합치에서 얻은 계수를 지정하면 Minitab에서는 가중 추세 분석을 수행합니다. 특정 계수에 대한 가중치가 α이면 Minitab에서는 다음과 같이 새 계수를 추정합니다.
공식
αp1 + (1 – α)p2
표기법
| 용어 | 설명 |
|---|---|
| p1 | 현재 데이터에서 추정된 계수 |
| p2 | 이전 계수 |
예측값
Minitab에서는 추세 방정식을 사용하여 특정 시간 값에 대한 예측값을 계산합니다. 예측시점 이전 데이터는 추세를 적합시키는 데 사용됩니다.
MAPE
평균 절대 백분율 오차(MAPE)는 적합된 시계열 값의 정확도를 측정합니다. MAPE는 정확도를 백분율로 표시합니다.
공식
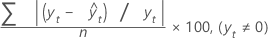
표기법
| 용어 | 설명 |
|---|---|
| yt | 시간 t에서의 실제 값 |
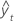 | 적합치 |
| n | 관측치 수 |
MAD
평균 절대 편차(MAD)는 적합된 시계열 값의 정확도를 측정합니다. MAD는 데이터와 같은 단위로 정확도를 표시하여 오차의 양을 개념화하는 데 사용됩니다.
공식
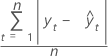
표기법
| 용어 | 설명 |
|---|---|
| yt | 시간 t에서의 실제 값 |
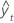 | 적합치 |
| n | 관측치 수 |
MSD
평균 제곱 편차(MSD)는 모형에 관계없이 항상 동일한 분모 n을 사용하여 계산됩니다. MSD는 매우 큰 예측 오차에 대해 MAD보다 더 민감한 측도입니다.
공식
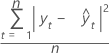
표기법
| 용어 | 설명 |
|---|---|
| yt | 시간 t에서의 실제 값 |
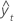 | 적합치 |
| n | 관측치 수 |
