이 항목의 내용
길이
시계열의 관측치 수입니다.
결측값 개수
시계열의 결측값 개수입니다.
적합된 추세 방정식
| 모형 유형 | 방정식 |
|---|---|
| 선형 | Yt = b0 + (b1 * t) |
| 2차 | Yt = b0+ b1 * t + (b2* t2) |
| 지수 성장 | Yt = b0 + (b1t) |
| S-곡선(Pearl-Reed 로지스틱) | Yt = (10a) / (b0 + b1 * b2t). |
- yt는 변수입니다.
- b0은 상수입니다.
- b1 및 b2는 계수입니다.
- t는 시간 단위의 값입니다.
MAPE
평균 절대 백분율 오차(MAPE)는 정확도를 오차의 백분율로 표시합니다. MAPE는 백분율이기 때문에 다른 정확도 측도 통계량보다 더 쉽게 이해할 수 있습니다. 예를 들어 MAPE가 5이면 예측 값은 평균 5% 벗어납니다.
그러나 모형이 데이터를 잘 적합시키는 것으로 보이더라도 MAPE 값이 아주 큰 경우도 있습니다. 0에 가까운 데이터 값이 있는지 확인하려면 그림을 조사하십시오. MAPE는 절대 오차를 실제 데이터로 나누기 때문에 0에 가까운 값이 있으면 MAPE가 상당히 크게 팽창할 수 있습니다.
해석
다른 시계열 모형의 적합치를 비교하는 데 사용하십시오. 값이 작을수록 적합도가 높습니다. 단일 모형에 3개의 정확도 측도 모두에 대한 가장 낮은 값이 없는 경우 MAPE가 일반적으로 많이 사용되는 측정값입니다.
정확도 측도는 한 주기 전 잔차를 기반으로 합니다. 각 시점에서 모형이 다음 시점에 대한 Y 값을 예측하기 위해 사용됩니다. 예측 값(적합치)과 실제 Y 간의 차이가 한 주기 전 잔차입니다. 이 때문에 정확도 측도는 데이터의 끝에서 1주기를 예측할 때 예상할 수 있는 정확도를 나타냅니다. 따라서 2주기 이상 예측하는 경우의 정확도는 나타내지 않습니다. 예측을 위해 모형을 사용하는 경우 정확도 측도만을 기준으로 결정을 내리지 말아야 합니다.
MAD
평균 절대 편차(MAD)는 데이터와 같은 단위로 정확도를 표시하므로 오차의 양을 판단하는 데 도움이 됩니다. MAD의 경우 MSD에 비해 특이치가 적은 영향을 미칩니다.
해석
다른 시계열 모형의 적합치를 비교하는 데 사용하십시오. 값이 작을수록 적합도가 높습니다.
정확도 측도는 한 주기 전 잔차를 기반으로 합니다. 각 시점에서 모형이 다음 시점에 대한 Y 값을 예측하기 위해 사용됩니다. 예측값(적합치)과 실제 Y 간의 차이가 한 주기 전 잔차입니다. 이 때문에 정확도 측도는 데이터의 끝에서 1주기를 예측할 때 예상할 수 있는 정확도를 나타냅니다. 따라서 2주기 이상 예측하는 경우의 정확도는 나타내지 않습니다. 예측을 위해 모형을 사용하는 경우 정확도 측도만을 기준으로 결정을 내리지 말아야 합니다. 또한 모형의 적합치를 조사하여 예측값과 모형이, 특히 계열의 끝에서 데이터를 가깝게 따르는지 확인해야 합니다.
MSD
평균 제곱 편차(MSD)는 적합 시계열 값의 정확도를 측정합니다. MSD의 경우 MAD에 비해 특이치가 큰 영향을 미칩니다.
해석
다른 시계열 모형의 적합치를 비교하는 데 사용하십시오. 값이 작을수록 적합도가 높습니다.
정확도 측도는 한 주기 전 잔차를 기반으로 합니다. 각 시점에서 모형이 다음 시점에 대한 Y 값을 예측하기 위해 사용됩니다. 예측값(적합치)과 실제 Y 간의 차이가 한 주기 전 잔차입니다. 이 때문에 정확도 측도는 데이터의 끝에서 1주기를 예측할 때 예상할 수 있는 정확도를 나타냅니다. 따라서 2주기 이상 예측하는 경우의 정확도는 나타내지 않습니다. 예측을 위해 모형을 사용하는 경우 정확도 측도만을 기준으로 결정을 내리지 말아야 합니다. 또한 모형의 적합치를 조사하여 예측값과 모형이, 특히 계열의 끝에서 데이터를 가깝게 따르는지 확인해야 합니다.
추세
추세 값은 적합치라고도 합니다. 추세 값은 시간 (t)에서 변수의 점 추정치입니다.
해석
추세 값은 데이터 집합의 각 관측치에 대한 특정 시간 값을 시계열 모형에 입력하여 계산됩니다.
예를 들어, 모형 방정식이 y = 5 + 10x이면 시간 2에서의 추세 값이 25 (25 = 5 + 10(2))입니다.
추세 값이 관측치와 매우 다른 관측은 비정상적이거나 영향력이 있을 수도 있습니다. 특이치의 원인을 식별해 보십시오. 모든 데이터 입력 또는 측정 오류를 수정하십시오. 비정상적인 일회성 사건과 연관된 데이터 값을 삭제해 보십시오(특수 원인). 그런 다음 분석을 반복하십시오.
추세 제거
추세 제거 값은 잔차라고도 합니다. 추세 제거 값은 관측값과 추세 값 간의 차이입니다.
해석
모형이 적절한지 확인하려면 추세 제거 값을 그림으로 표시하십시오. 값을 조사하면 모형이 데이터에 얼마나 잘 적합되는 지에 대한 유용한 정보를 얻을 수 있습니다. 일반적으로 추세 제거 값은 분명한 패턴이나 비정상적인 값 없이 0 주위에 랜덤하게 분포해야 합니다.
기간
Minitab에서는 사용자가 예측값을 생성하는 기간을 표시합니다. 기간은 예측값의 시간 단위입니다. 기본적으로 예측값은 데이터의 끝에서 시작합니다.
예측
예측값은 시계열 모형에서 얻은 적합치입니다. Minitab에서는 사용자가 지정한 수의 예측값을 표시합니다. 예측값은 데이터의 끝 또는 사용자가 지정한 원점에서 시작됩니다. Minitab에서는 원점 전의 데이터를 사용하여 적합된 추세 방정식의 계수를 계산합니다. 원점을 지정하는 경우 Minitab에서는 해당 열 번호까지의 데이터만 예측값에 사용합니다.
해석
지정된 기간 동안 변수를 예측하려면 예측값을 사용합니다. 예를 들어, 창고 관리자는 이전 60개월 간의 주문을 바탕으로 향후 3개월 동안 얼마나 많은 제품을 주문해야 하는지 모형화할 수 있습니다.
예측값이 정확할지 여부를 확인하려면 추세 분석 그림의 끝 및 예측값을 조사하십시오. 적합치는 특히 계열의 끝에서 데이터를 가깝게 따라야 합니다. 적합치가 계열의 끝에서 데이터로부터 멀어지기 시작하면 기본 추세가 변경될 수도 있습니다. 추세가 변경되면 모형이 정확한 예측값을 생성하지 못할 수도 있습니다. 이 경우 장기간 추세가 일관되지 않은지 여부를 확인하려면 더 많은 데이터를 수집하십시오.
예측값이 정확해 보이더라도 향후 3기간 이상의 예측값에 대해서는 주의하십시오. 짧은 기간의 데이터에서 관측된 추세는 더 큰 주기의 일부일 수 있으며 앞으로는 계속되지 않을 수도 있습니다. 추세는 급변할 수도 있으므로 일반적으로 향후 2 또는 3기간만 예측해야 합니다.
추세 분석 그림
추세 분석 그림은 관측치 대 시간을 표시합니다. 이 그림에는 적합된 추세 방정식에서 계산된 적합치, 예측 값 및 정확도 측도가 포함됩니다.
해석
- 모형이 데이터에 적합하면 이중 지수 평활을 수행하고 두 모형을 비교할 수 있습니다.
- 모형이 데이터를 적합하지 않는 경우에는 분석을 다시 수행하고 다른 유형의 모형을 선택하십시오. 선형 모형을 적합하고 데이터에 곡면성이 보이는 경우 2차, 지수 또는 S-곡선 모형을 선택하십시오. 어느 모형도 데이터를 적합하지 않으면 다른 시계열 분석을 사용하십시오. 자세한 내용은 어떤 시계열 분석을 사용해야 합니까?에서 확인하십시오.
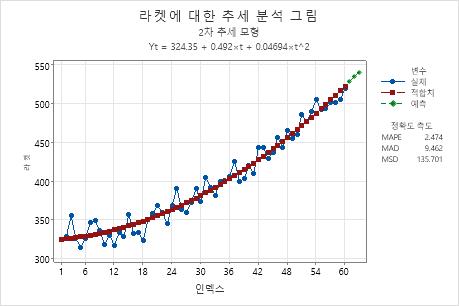
이 추세 분석 그림에서는 적합치가 데이터를 가깝게 따르며, 이는 모형이 데이터에 적합하다는 것을 나타냅니다.
곡선 모수
- 절편
- 시간 = 0에서 모형의 값입니다. 절편은 10a / (β0 + β1)과 같습니다.
- 점근선
- 시간이 무한대로 증가함에 따라 모형이 접근하는 값입니다. 점근선은 10a / β0과 같습니다.
- 점근율
- 모형이 점근선에 접근하는 비율입니다. 값이 낮을수록 모형이 점근선에 더 빠르게 접근합니다. 점근율은 β2와 같습니다.
잔차의 히스토그램
잔차의 히스토그램은 모든 관측치에 대한 잔차의 분포를 보여줍니다. 모형이 데이터를 잘 적합시키는 경우, 잔차가 0을 평균으로 랜덤하게 분포해야 합니다. 따라서 히스토그램이 0을 중심으로 거의 대칭이어야 합니다.
잔차의 정규 확률도
잔차의 정규 확률도는 분포가 정규 분포일 때 잔차 대 잔차의 기대값을 표시합니다.
해석
잔차의 정규 확률도를 사용하면 잔차가 정규 분포를 따르는지 여부를 확인할 수 있습니다. 그러나 이 분석에서는 잔차가 정규 분포를 따르지 않아도 됩니다.
S-곡선은 긴 꼬리를 갖는 분포를 의미합니다.
역 S-곡선은 짧은 꼬리를 갖는 분포를 의미합니다.
하향 곡선은 오른쪽으로 치우친 분포를 의미합니다.
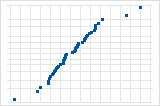
선으로부터 멀리 떨어져 있는 몇 개의 점은 특이치를 갖는 분포를 암시합니다.
잔차 대 적합치
잔차 대 적합치 그림은 y-축에 잔차, x-축에 적합치를 표시합니다.
해석
잔차 대 적합치 그림을 사용하면 잔차가 치우치지 않고 분산이 일정한지 여부를 확인할 수 있습니다. 이상적으로는 점들이 식별 가능한 패턴 없이 0의 양쪽에 랜덤하게 분포해야 합니다.
| 패턴 | 패턴이 나타내는 내용 |
|---|---|
| 적합치에 대해 잔차가 부채꼴 모양으로 흩어져 있거나 고르지 않게 퍼져 있음 | 일정하지 않은 분산 |
| 곡선 | 고차 항 누락 |
| 한 점이 0에서 멀리 떨어져 있음 | 특이치 |
잔차에 일정하지 않은 분산이나 패턴이 있으면 예측값이 정확하지 않을 수도 있습니다.
잔차 대 순서
잔차 대 순서 그림은 잔차를 데이터가 수집된 순서대로 표시합니다.
해석
잔차 대 순서 그림을 사용하면 적합치가 관측 기간 동안의 관측치와 비교하여 얼마나 정확한지 확인할 수 있습니다. 점들의 패턴은 모형이 데이터에 적합하지 않다는 것을 나타낼 수도 있습니다. 이상적으로는 그림의 잔차들이 중심선 주위에 랜덤하게 분포해야 합니다.
| 패턴 | 패턴이 나타내는 내용 |
|---|---|
| 일관된 장기 추세 | 모형이 데이터에 적합함 |
| 단기 추세 | 이동 또는 패턴의 변화 |
| 한 점이 다른 점들로부터 멀리 떨어져 있음 | 특이치 |
| 점들의 급격한 이동 | 데이터의 기본 패턴이 변경됨 |
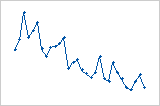
관측치의 순서가 왼쪽에서 오른쪽으로 증가함에 따라 잔차가 규칙적으로 줄어듭니다.
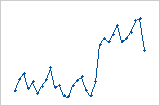
잔차 값이 작은 값(왼쪽 부분)에서 큰 값(오른쪽 부분)으로 갑자기 변경됩니다.
잔차 대 변수
잔차 대 변수 그림은 잔차 대 다른 변수를 표시합니다.
해석
그림을 사용하면 변수가 체계적인 방식으로 반응에 영향을 미치는지 여부를 확인할 수 있습니다. 잔차에 패턴이 존재하면 다른 변수가 반응에 연관됩니다. 이 정보를 다른 연구의 기초로 사용할 수 있습니다.
추세선 간 비교
참고
Minitab에서는 새 선을 사용하여 예측값을 계산합니다.
