이동 평균[MA]에 대한 방법 및 공식

이동 평균[MA]을 계산하기 위해 Minitab에서 계열 내 관측치의 연속적 그룹의 평균을 구합니다. 예를 들어, 계열이 숫자 4, 5, 8, 9, 10으로 시작하고 길이가 3인 이동 평균[MA]을 사용한다고 가정합니다. 이동 평균의 세 번째 값은 4, 5, 8의 평균, 네 번째 값은 5, 8, 9의 평균, 다섯 번째 값은 8, 9, 10의 평균입니다.

기본적으로 이동 평균[MA] 값은 해당 값이 계산되는 기간에 배치됩니다. 예를 들어, 이동 평균[MA] 길이가 3인 경우 첫 번째 숫자 이동 평균[MA] 값은 기간 3에 배치되고 그 다음 이동 평균[MA] 값은 기간 4에 배치되는 식입니다.

이동 평균[MA]을 중심화하면 범위의 끝이 아니라 중심에 이동 평균[MA]이 배치됩니다. 이동 평균[MA]의 중심화는 이동 평균[MA] 값을 중심이 되는 시점에 배치하기 위해 수행됩니다.

이동 평균[MA] 길이가 홀수인 경우

이동 평균[MA] 길이가 3이라고 가정합니다. 이 경우, Minitab에서는 첫 번째 숫자 이동 평균[MA] 값을 기간 2, 다음 값을 기간 3에 배치하고, 이런 식으로 계속합니다. 이 경우 첫 번째 기간과 마지막 기간의 이동 평균[MA] 값은 결측값( *)이 됩니다.

이동 평균[MA] 길이가 짝수인 경우

이동 평균[MA] 길이가 4라고 가정합니다. 기간 2.5에는 이동 평균[MA] 값을 배치할 수 없기 때문에 Minitab에서는 처음 네 값의 평균을 계산하고 MA1 이름을 지정합니다. 그런 다음 Minitab에서는 다음 네 값의 평균을 계산하고 MA2 이름을 지정합니다. 이 두 값의 평균이 Minitab에서 기간 3에 배치하는 숫자입니다 이 경우 처음 두 기간과 마지막 두 기간의 이동 평균[MA] 값은 결측값( *)이 됩니다.

시간 t에서의 적합치는 시간 t – 1에서의 중심화되지 않은 이동 평균[MA]입니다. 예측값은 예측시점에서의 적합치입니다. 10 시간 단위 이후를 예측할 경우 각 시간에 대해 예측된 값은 예측시점에서의 적합치가 됩니다. 이동 평균[MA]을 계산하는 데는 예측시점까지의 데이터가 사용됩니다.

연속적 이동 평균[MA]으로 선형 이동 평균[MA] 방법을 사용할 수 있습니다. 이 방법은 데이터에 추세 성분이 있는 경우에 자주 사용됩니다. 먼저 원래 계열의 이동 평균[MA]을 계산하고 저장합니다. 그런 다음 이전에 저장한 열의 이동 평균[MA]을 계산하고 저장하여 두 번째 이동 평균[MA]을 구합니다.

단순 예측에서 시간 t에 대한 예측값은 시간 t – 1에서의 데이터 값입니다. 이동 평균[MA] 길이를 1로 하여 이동 평균[MA] 절차를 사용하면 단순 예측이 됩니다.

공식

상한 = 예측값 + 1.96 ×

하한 = 예측값 – 1.96 ×

표기법

평균 절대 백분율 오차(MAPE)는 적합된 시계열 값의 정확도를 측정합니다. MAPE는 정확도를 백분율로 표시합니다.

공식

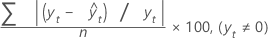
표기법

용어	설명
yt	시간 t에서의 실제 값
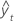	적합치
n	관측치 수

평균 절대 편차(MAD)는 적합된 시계열 값의 정확도를 측정합니다. MAD는 데이터와 같은 단위로 정확도를 표시하여 오차의 양을 개념화하는 데 사용됩니다.

공식

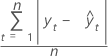
표기법

용어	설명
yt	시간 t에서의 실제 값
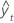	적합치
n	관측치 수

평균 제곱 편차(MSD)는 모형에 관계없이 항상 동일한 분모 n을 사용하여 계산됩니다. MSD는 매우 큰 예측 오차에 대해 MAD보다 더 민감한 측도입니다.

공식

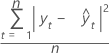
표기법

용어	설명
yt	시간 t에서의 실제 값
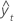	적합치
n	관측치 수