평가하려는 모델에 적합한 단계를 따릅니다. 단계는 계절 및 비 계절 모델의 경우 동일하지만 세부 사항은 다릅니다.
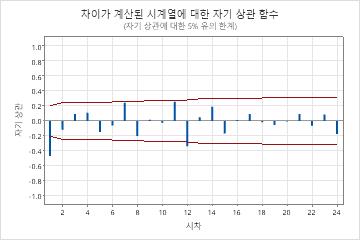
비계절적 ARIMA 모델에 적합
다음 단계를 완료하여 비계절 ARIMA 모델로 분석할 데이터 열을 지정합니다. 일정한 항을 가진 모델을 적합시키면 후보 모델의 p + q ≤ 9가 있습니다. 상수 항이 없는 모형을 맞추면 후보 모델의 p + q ≤ 10이 됩니다. d = 2인 후보 모델은 일정한 항이 없는 경우 적합합니다.
전제 조건
일반적으로 변환의 필요성을 평가하고 이 분석을 시작하기 전에 차이점 보관 순서를 결정합니다.
변환
시계열 플롯을 사용하여 시계열의 분산이 고정되어 있는지 확인합니다. 시계열에 점의 스프레드에 패턴이 있으면 분산은 고정되어 있지 않습니다. 시계열의 Box-Cox 변환을 사용하여 계열의 분산을 고정시킵니다. 시계열에 대한 Box-Cox 변환을 평가하려면 을 선택합니다 통계분석 > 시계열 > Box-Cox 변환. 에서 최상의 ARIMA
모형으로 예측Box-Cox 변환 사용에 대한 자세한 내용은 을 참조하십시오 에 대한 분석 옵션 선택최상의 ARIMA 모형으로 예측.
차이점 보관용
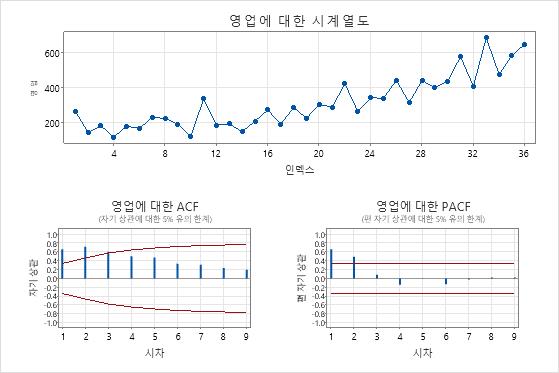
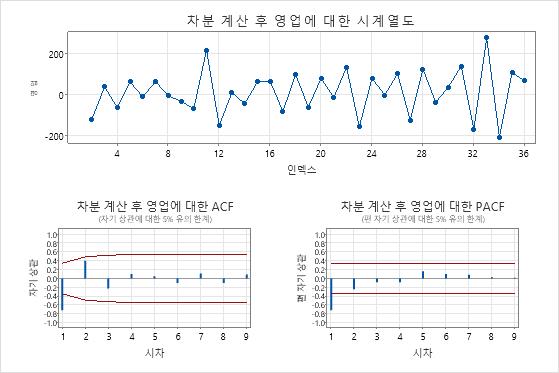
계열에 대한 ACF(자기상관 함수)의 플롯을 검사하여 차이점 보관의 순서를 결정합니다. 차이점 보관의 필요성을 보여주는 ACF 플롯의 일반적인 패턴은 천천히 감소하는 추세입니다. 데이터가 추가 차이점 보관을 지원하는 경우 차이 있는 데이터의 ACF에서 동일한 패턴이 발생합니다. 자기 상관 분석을 수행하려면 을 선택하십시오통계분석 > 시계열 > 자기
상관. 또한 주문을 결정하기 위해 증강 된 Dickey-Fuller 테스트를 고려하십시오. 모델을 평가할 때 차이점 보관용 순서를 지정합니다.
추세가 있는 시계열의 ACF 플롯
이 결과에서 원본 데이터의 시계열 그림은 명확한 추세를 보여줍니다. 차이난 데이터의 시계열 그림은 연속적인 값 간의 차이를 보여줍니다. 차이가 있는 데이터는 점들이 변동에서 명백한 패턴 없이 수평 경로를 따르기 때문에 고정되어 나타납니다.
ACF 플롯은 또한 차이점 보관의 효과를 보여줍니다. 이 결과에서 원본 데이터의 ACF 플롯은 지연에 걸쳐 천천히 감소된 스파이크를 보여줍니다. 이 패턴은 데이터가 고정되어 있지 않음을 나타냅니다. 차이 데이터의 ACF 플롯에서 0과 유의하게 다른 스파이크는 지연 1에 있습니다.
비계절 모델 평가
에 시계열 정기적으로 수집되고 시간순으로 기록된 수치 데이터의 열을 입력합니다.
에서 차분 순서 d비계절적 차이 보관용 순서를 선택합니다.
에서 자동 회귀 순서 p평가할 최소값과 평가할 최대값을 선택합니다. 이 분석은 선택 항목에서 자동 회귀 및 이동 평균 주문의 모든 조합과 함께 모델을 적합하게 만듭니다. 최소값과 최대값에 동일한 값을 입력하면 분석에서 모든 후보 모델에 대해 해당 값을 사용합니다.
에서 이동 평균 순서 q평가할 최소값과 평가할 최대값을 선택합니다. 이 분석은 선택 항목에서 자동 회귀 및 이동 평균 주문의 모든 조합과 함께 모델을 적합하게 만듭니다. 최소값과 최대값에 동일한 값을 입력하면 분석에서 모든 후보 모델에 대해 해당 값을 사용합니다.
모델에 상수 항을 포함하도록 선택합니다 모형에 상수 항 포함 . 상수 항을 사용하면 평균이 0이 아닌 계열을 추정할 수 있습니다. 일정한 항이 없으면 모형이 맞는 계열의 평균은 0입니다. 분석이 상수 항이 있는 모형을 맞출 수 없는 경우 분석은 상수 항 없이 모형을 맞추려고 시도합니다.
에 예측 수 예측하려는 연속된 기간의 수를 입력합니다. 일반적으로 원하는 예측을 제공하기 위해 최소 숫자를 입력합니다. 예를 들어 월별 데이터가 있고 시리즈가 끝난 후 6개월 동안 예측을 가져오려면 6을 입력합니다.
시계열의 끝에서 예측 또는 시계열의 K번째 값에서 예측을 선택합니다. 사용자가 값을 입력하면 Minitab에서는 해당 열 번호까지의 데이터만 예측 값에 사용합니다. Minitab에서는 모든 데이터를 사용하여 적합치를 계산하기 때문에 예측값은 적합치와 다릅니다. 예를 들어, 한 분석가가 1월부터 12월까지 5년 간의 월별 데이터를 가지고 있습니다. 분석가는 다음 달에 대한 예측값을 생성하려고 하지만 마지막 12월의 데이터가 불안전합니다. 분석가는 시리즈의 59번째 값에서 예측을 지정하고 두 개의 예측을 지정합니다. 이 분석은 처음 59개월 동안의 데이터를 사용하여 12월과 1월에 대한 예측을 생성합니다.
ARIMA 모델을 사용하여 예측하기 전에 모형이 데이터를 잘 맞는지 확인합니다. 잔차 진단을 검사하여 모형이 ARIMA 모델에 대한 가정을 충족하는지 여부를 확인합니다. 자세한 내용은 에 대한 주요 결과 해석최상의 ARIMA 모형으로 예측(으)로 이동하십시오.
계절별 ARIMA 모델에 적합
다음 단계를 완료하여 계절별 ARIMA 모델로 분석할 데이터 열을 지정합니다. 일정한 항을 가진 모형을 적합시키면 후보 모형의 p + q + P + Q ≤ 9가 있습니다. 일정한 항이 없는 모형을 적합시키면 후보 모델의 p + q + P + Q ≤ 10이 됩니다. d + D > 1 인 후보 모델은 일정한 항없이 적합합니다.
전제 조건
일반적으로 변환의 필요성을 평가하고 이 분석을 시작하기 전에 차이점 보관 순서를 결정합니다.
변환
시계열 플롯을 사용하여 시계열의 분산이 고정되어 있는지 확인합니다. 시계열에 점의 스프레드에 패턴이 있으면 분산은 고정되어 있지 않습니다. 시계열의 Box-Cox 변환을 사용하여 계열의 분산을 고정시킵니다. 시계열에 대한 Box-Cox 변환을 평가하려면 을 선택합니다 통계분석 > 시계열 > Box-Cox 변환. 에서 최상의 ARIMA
모형으로 예측Box-Cox 변환 사용에 대한 자세한 내용은 을 참조하십시오 에 대한 분석 옵션 선택최상의 ARIMA 모형으로 예측.
차이점 보관용
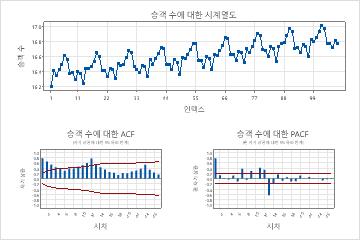
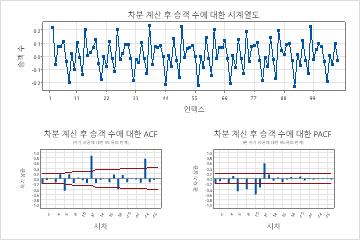
계열에 대한 자기상관 함수(ACF)의 플롯을 검사하여 차이점 보관의 비계절 및 계절적 순서를 결정합니다. 각 k번째 기간을 반복하는 계절 패턴은 패턴의 일부를 제거하기 위해 k번째 차이를 취해야 함을 나타냅니다. 천천히 감소하는 추세는 계절적 차이가 아닌 차이도 사용해야 함을 나타냅니다. 데이터가 추가 차이점 보관을 지원하는 경우 차이 있는 데이터의 ACF에서 동일한 패턴이 발생합니다. 계절적 차이 보관용 주문이 1보다 큰 경우는 드뭅니다. 자기 상관 분석을 수행하려면 을 선택하십시오통계분석 > 시계열 > 자기
상관. 모델을 평가할 때 차이점 보관용 순서를 지정합니다.
추세와 계절 패턴이 있는 시계열의 ACF 플롯
이 결과에서 원본 데이터의 시계열 그림은 상승 추세와 주기가 12인 계절 패턴을 보여 줍니다. 차이난 데이터의 시계열 그림은 연속적인 값 간의 차이를 보여줍니다.
차이 후 데이터에 대한 ACF 플롯은 비계절적 차이 보관의 효과를 보여줍니다. 이 결과에서 원본 데이터의 ACF 플롯은 지연에 걸쳐 천천히 감소된 스파이크를 보여줍니다. 스파이크는 계절적 지연에도 나타납니다. 이 두 패턴은 데이터가 고정되어 있지 않음을 나타냅니다. 비계절적 차이 보관 후 데이터의 ACF 플롯에서 상당한 스파이크는 계절적 지연에 있습니다.
계절 차이와 비계절적 차이 이후의 데이터의 ACF 플롯은 계절 패턴을 표시하지 않습니다. 이러한 데이터에 적합한 차이점 보관의 순서는 1 개의 비 계절 차이와 1 계절 차이입니다.
계절 모델 평가
에 시계열 정기적으로 수집되고 시간순으로 기록된 수치 데이터의 열을 입력합니다.
에서 차분 순서 d비계절적 차이 보관용 순서를 선택합니다.
에서 자동 회귀 순서 p평가할 최소값과 평가할 최대값을 선택합니다. 이 분석은 선택 항목에서 자동 회귀 및 이동 평균 주문의 모든 조합과 함께 모델을 적합하게 만듭니다. 최소값과 최대값에 동일한 값을 입력하면 분석에서 모든 후보 모델에 대해 해당 값을 사용합니다.
에서 이동 평균 순서 q평가할 최소값과 평가할 최대값을 선택합니다. 이 분석은 선택 항목에서 자동 회귀 및 이동 평균 주문의 모든 조합과 함께 모델을 적합하게 만듭니다. 최소값과 최대값에 동일한 값을 입력하면 분석에서 모든 후보 모델에 대해 해당 값을 사용합니다.
계절 패턴의 길이를 선택하고 기간이 있는 계절별 모형 적합 입력합니다. 예를 들어, 월별로 데이터를 수집하고 데이터에 연간 패턴이 있는 경우 12를 입력하십시오.
에서 계절별 차분 순서 D계절 차이 보관용 순서를 선택합니다. 계절 패턴을 가진 대부분의 시리즈는 데이터를 고정시키기 위해 계절별 차순의 차이점을 사용합니다. 대부분의 계절적 패턴의 경우 1이면 충분합니다.
에서 자동 회귀 순서 P평가할 최소값과 평가할 최대값을 선택합니다. 이 분석은 선택 항목에서 자동 회귀 및 이동 평균 주문의 모든 조합과 함께 모델을 적합하게 만듭니다. 최소값과 최대값에 동일한 값을 입력하면 분석에서 모든 후보 모델에 대해 해당 값을 사용합니다.
에서 이동 평균 순서 Q평가할 최소값과 평가할 최대값을 선택합니다. 이 분석은 선택 항목에서 자동 회귀 및 이동 평균 주문의 모든 조합과 함께 모델을 적합하게 만듭니다. 최소값과 최대값에 동일한 값을 입력하면 분석에서 모든 후보 모델에 대해 해당 값을 사용합니다.
모델에 상수 항을 포함하도록 선택합니다 모형에 상수 항 포함 . 상수 항을 사용하면 평균이 0이 아닌 계열을 추정할 수 있습니다. 일정한 항이 없으면 모형이 맞는 계열의 평균은 0입니다. 분석이 상수 항이 있는 모형을 맞출 수 없는 경우 분석은 상수 항 없이 모형을 맞추려고 시도합니다.
에 예측 수 예측하려는 연속된 기간의 수를 입력합니다. 일반적으로 원하는 예측을 제공하기 위해 최소 숫자를 입력합니다. 예를 들어 월별 데이터가 있고 시리즈가 끝난 후 6개월 동안 예측을 가져오려면 6을 입력합니다.
시계열의 끝에서 예측 또는 시계열의 K번째 값에서 예측을 선택합니다. 사용자가 값을 입력하면 Minitab에서는 해당 열 번호까지의 데이터만 예측 값에 사용합니다. Minitab에서는 모든 데이터를 사용하여 적합치를 계산하기 때문에 예측값은 적합치와 다릅니다. 예를 들어, 한 분석가가 1월부터 12월까지 5년 간의 월별 데이터를 가지고 있습니다. 분석가는 다음 달에 대한 예측값을 생성하려고 하지만 마지막 12월의 데이터가 불안전합니다. 분석가는 시리즈의 59번째 값에서 예측을 지정하고 두 개의 예측을 지정합니다. 이 분석은 처음 59개월 동안의 데이터를 사용하여 12월과 1월에 대한 예측을 생성합니다.
