에 대한 주요 결과 해석최상의 ARIMA 모형으로 예측

다음 단계를 완료하여 모델 선택 프로세스와 ARIMA 분석의 결과를 해석합니다. 주요 결과에는 모델 선택 통계, p-값, 계수, Ljung-Box 카이-제곱 통계량 및 잔차의 자기 상관 함수가 포함됩니다.

이 항목의 내용

1단계: 대체 모델 고려
2단계: 모형의 각 항이 유의한지 여부 확인
3단계: 모형이 분석의 가정을 충족하는지 여부 확인

1단계: 대체 모델 고려

모델 선택 테이블에는 검색의 각 모델에 대한 기준이 표시됩니다. 표에는 p가 자동 회귀 항이고, d가 차이점 보관용 항이고, q가 이동 평균 항인 항의 순서가 표시됩니다. 계절 용어는 대문자를 사용하고 계절이 아닌 용어는 소문자를 사용합니다.

여러 모형을 비교하려면 AIC, AICc 및 BIC를 사용합니다. 작은 값을 사용하는 것이 바람직합니다. 그러나 항 집합에 대해 값이 가장 적은 모형이 반드시 데이터를 잘 맞지는 않습니다. 검정 및 플롯을 사용하여 모형이 데이터를 얼마나 잘 적합시키는지 평가합니다. 기본적으로 ARIMA 결과는 AICc 값이 가장 높은 모델에 대한 것입니다.

모델 선택 테이블이 포함된 대화상자를 열려면 선택합니다 대체 모델 선택 . 조건을 비교하여 성능이 비슷한 모델을 조사합니다.

ARIMA 출력을 사용하여 모형의 항이 통계적으로 유의하고 모형이 분석의 가정을 충족하는지 확인합니다. 테이블의 모델이 데이터에 잘 맞지 않으면 차이점 보관 순서가 다른 모델을 고려하십시오.

또한 대체 모델이 거의 최상의 모델뿐만 아니라 성능이 뛰어나고 자동 회귀 및 이동 평균 항의 순서가 낮은 경우 대체 모델을 고려하십시오. 용어가 적은 모델은 해석하기가 더 쉽고 예측 능력이 더 뛰어납니다. 용어가 적은 모델도 중복 용어를 포함할 가능성이 적습니다. 예를 들어, 계절적 자동 회귀 항은 때때로 계절적 이동 평균 항과 중복됩니다. 중복 항은 때때로 계수의 추정치를 불안정하게 만듭니다. 다음은 불안정적인 계수의 일부 결과입니다.

예측 변수와 반응 간에 유의한 관계가 존재하는 경우에도 계수가 유의하지 않은 것으로 보일 수 있습니다.
높은 상관 관계가 있는 예측 변수에 대한 계수는 표본에 따라 크게 달라질 수 있습니다.
높은 상관 관계가 있는 모형 항을 제거하면 높은 상관 관계가 있는 다른 항의 추정 계수에 크게 영향을 미칩니다. 높은 상관 관계가 있는 항의 계수 부호가 잘못되었을 수도 있습니다.

* 경고 * 상수 항을 포함하지 않는 추정 불가능한 ARIMA(p, d, q) 모형:
(2, 1, 2)

모형 선택

모델(d = 1)	로그 우도	AICc	AIC	BIC
p = 0, q = 2*	-197.052	400.878	400.103	404.769
p = 1, q = 2	-196.989	403.311	401.978	408.199
p = 1, q = 0	-201.327	407.029	406.654	409.765
p = 2, q = 0	-200.239	407.251	406.477	411.143
p = 1, q = 1	-200.440	407.655	406.880	411.546
p = 2, q = 1	-201.776	412.884	411.551	417.773
p = 0, q = 1	-204.584	413.542	413.167	416.278
p = 0, q = 0	-213.614	429.350	429.229	430.784

주요 결과 AICc, BIC 및 AIC

ARIMA (0, 1, 2)는 AICc의 최상의 가치를 가지고 있습니다. 다음 ARIMA 결과는 ARIMA(0, 1, 2) 모델에 대한 것입니다. 모델이 데이터를 충분히 잘 맞지 않으면 ARIMA(1, 1, 2) 모델 및 ARIMA(1, 1, 1) 모델과 같이 성능이 유사한 다른 모델을 고려합니다. 데이터를 충분히 잘 맞는 모델이 없는 경우 다른 유형의 모델을 사용할지 여부를 고려합니다.

2단계: 모형의 각 항이 유의한지 여부 확인

반응과 모형의 각 항 간의 연관성이 통계적으로 유의한지 여부를 확인하려면 항에 대한 p-값을 유의 수준과 비교하여 귀무 가설을 평가합니다. 귀무 가설은 항이 0과 유의하게 다른지 않다는 것이며, 이는 항과 반응 사이에 연관성이 없다는 것을 나타냅니다. 일반적으로 0.05의 유의 수준(α 또는 알파로 표시됨)이 적절합니다. 0.05의 유의 수준은 항이 0과 유의하게 다른데 0과 유의하게 다르지 않다고 결론을 내릴 위험이 5%라는 것을 나타냅니다.

P-값 ≤ α: 이 용어는 통계적으로 유의합니다.: p-값이 유의 수준보다 작거나 같으면 계수가 통계적으로 유의하다는 결론을 내릴 수 있습니다.
P-값 > α: 이 용어는 통계적으로 유의하지 않습니다.: p-값이 유의 수준보다 크면 계수가 통계적으로 유의하다는 결론을 내릴 수 없습니다. 항 없이 모형을 다시 적합시킬 수도 있습니다.

모수의 최종 추정치

유형	계수	SE 계수	T-값	P-값
AR 1	-0.504	0.114	-4.42	0.000
상수	150.415	0.325	463.34	0.000
평균	100.000	0.216

주요 결과: P, 코프

자기회귀 항의 p-값이 유의 수준 0.05보다 작습니다. 자기회귀 항에 대한 계수가 통계적으로 유의하다는 결론을 내릴 수 있으며, 모형의 항을 유지해야 합니다.

3단계: 모형이 분석의 가정을 충족하는지 여부 확인

Ljung-Box 카이-제곱 통계량 및 잔차의 자기상관함수를 사용하면 모형이 잔차가 서로 독립적이라는 가정을 충족하는지 여부를 확인할 수 있습니다. 가정이 충족되지 않으면 모형이 데이터에 적합하지 않은 것이므로 결과를 해석할 때 주의해야 합니다.

Ljung-Box 카이-제곱 통계량: 잔차가 서로 독립적인지 여부를 확인하려면 p-값을 각 카이 제곱 통계량에 대한 유의 수준과 비교하십시오. 일반적으로 0.05의 유의 수준(α 또는 알파로 표시됨)이 적절합니다. p-값이 유의 수준보다 크면 잔차가 서로 독립적이고 모형이 가정을 충족한다는 결론을 내릴 수 있습니다.
잔차의 자기상관함수: 유의한 상관 관계가 존재하지 않으면 잔차가 서로 독립적이라는 결론을 내릴 수 있습니다. 그러나 계절적 시차가 아닌 고차 항 시차에서 1개 또는 2개의 유의한 상관이 있을 수 있습니다. 이러한 상관은 일반적으로 랜덤 오차에 의해 발생하며 가정이 충족되지 않는다는 징후는 아닙니다. 이 경우 잔차가 서로 독립적이라는 결론을 내릴 수 있습니다.

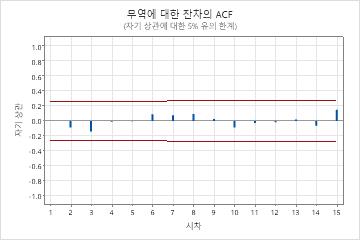
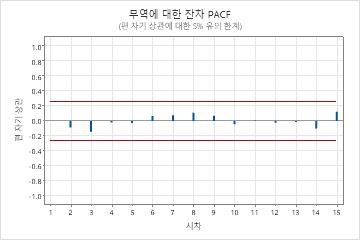
주요 결과: p-값, 잔차 ACF
이 결과에서 Ljung-Box 카이-제곱 통계량에 대한 p-값은 모두 0.05보다 크고 잔차의 자기상관함수에 대한 어느 상관도 유의하지 않습니다. 모형이 잔차가 서로 독립적이라는 가정을 충족한다는 결론을 내릴 수 있습니다.

시차	12	24	36	48
카이-제곱	4.05	12.13	25.62	32.09
DF	10	22	34	46
P-값	0.945	0.955	0.849	0.940