이 항목의 내용
데이터 입력
변수에 정기적으로 수집되고 시간순으로 기록된 수치 데이터의 열을 입력합니다. 데이터가 여러 열에 있는 경우(예를 들어, 별도의 열에 각 연도에 대한 데이터가 있는 경우) 데이터를 단일 열에 쌓아야 합니다.
이 워크시트의 판매량에는 매월 판매되는 컴퓨터의 수가 포함됩니다.
| C1 |
|---|
| 판매량 |
| 195000 |
| 213330 |
| 208005 |
| 249000 |
| 237040 |
평활에 사용할 가중치
가중치는 각 성분이 현재 조건에 반응하는 방식을 정의하여 평활의 양을 조정합니다. 일반적으로 데이터를 충분히 평활화하여 잡음(불규칙한 변동)을 줄여 패턴이 더 분명하게 보이도록 해야 합니다. 그러나 데이터를 너무 많이 평활화하여 중요한 상세 정보가 유실되는 일은 없도록 해야 합니다.
적절한 가중치를 모를 경우 최적 ARIMA을 선택하십시오. 그런 다음, 시계열도를 조사한 후 가중치를 늘리거나 줄일 수 있습니다. 가중치가 더 낮을수록 선이 더 평활화되고 가중치가 더 높을수록 선이 덜 평활화됩니다. 평활값이 잡음과 함께 변동하지 않도록 잡음 데이터에 대해 더 작은 가중치를 사용하십시오.
- 최적 ARIMA
- Minitab에서는 ARIMA (0,2,2) 모형에서 잔차 제곱합을 최소화하는 가중치를 사용합니다. ARIMA (0,2,2) 모형은 데이터의 두 번째 차이를 계산하며 2차 이동 평균[MA] 항을 포함합니다.
- 지정된 가중치
-
두 평활화 가중치 모두의 값을 입력합니다.
- 수준용
- 수준은 관측치의 이동 평균[MA]과 유사합니다. 일반적으로 0과 1 사이의 수준 가중치가 적절합니다.
- 추세용
- 추세는 연속 관측치 간 차이의 이동 평균[MA]과 유사합니다. 일반적으로 0과 1 사이의 추세 가중치가 적절합니다.
가중치가 낮을수록 최근 데이터에 가중치를 덜 부여하므로 예측값(녹색)이 전반적인 추세를 따릅니다.
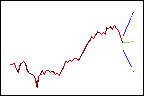
추세 = 0.03
가중치가 높을수록 최근 데이터에 가중치를 더 부여하므로 예측값이 데이터의 끝에서 추세를 따릅니다.
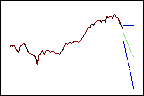
추세 = 0.80
예측 생성
시계열에 대한 예측값을 생성하려면 다음 단계를 수행하십시오.
- 예측 생성을 선택합니다.
- 예측 수에 예측하려는 연속된 기간의 수를 입력합니다.
- 예측 시점에 첫 번째 예측값에 대한 행 번호를 지정합니다. 이 필드를 비워둘 경우 Minitab에서는 시계열의 끝에서 예측값을 시작합니다.
사용자가 값을 입력하면 Minitab에서는 해당 열 번호까지의 데이터만 예측 값에 사용합니다. Minitab에서는 모든 데이터를 사용하여 적합치를 계산하기 때문에 예측값은 적합치와 다릅니다.
예를 들어, 한 분석가가 1월부터 12월까지의 월별 데이터를 가지고 있습니다. 분석가는 12월에 다음 달에 대한 예측값을 생성하려고 하지만, 12월의 데이터가 불안전합니다. 분석가는 예측 수에 2를 입력하고 예측 시점에 12를 입력합니다. Minitab에서는 11월까지의 데이터를 사용하여 12월과 1월에 대한 예측값을 생성합니다.
