1단계: 모형이 데이터에 적합한지 여부 확인
- 모형이 데이터에 적합하면 추세 분석을 수행하고 두 모형을 비교할 수 있습니다.
- 모형이 데이터에 적합하지 않으면 그림에서 계절성이 있거나 추세가 결여되었는지 조사하십시오. 계절성이 있거나 추세가 결여된 증거가 보이면 다른 시계열 분석을 사용해야 합니다. 자세한 내용은 어떤 시계열 분석을 사용해야 합니까?에서 확인하십시오.
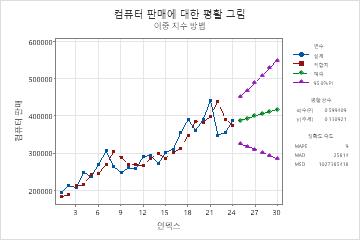
이 평활 그림에서는 적합치가 데이터를 가깝게 따르며, 이는 모형이 데이터에 적합하다는 것을 나타냅니다.
2단계: 모형의 적합치를 다른 모형과 비교
참고
정확도 측도는 데이터 끝에서 1주기를 예측할 때 예상할 수 있는 정확도를 나타냅니다. 따라서 2주기 이상 예측하는 경우의 정확도는 나타내지 않습니다. 예측을 위해 모형을 사용하는 경우 정확도 측도만을 기준으로 결정을 내리지 말아야 합니다. 또한 모형의 적합치를 조사하여 예측값과 모형이, 특히 계열의 끝에서 데이터를 가깝게 따르는지 확인해야 합니다.
모형 1
정확도 측도
| MAPE | 7.265 |
|---|---|
| MAD | 16.621 |
| MSD | 518.119 |
모형 2
정확도 측도
| MAPE | 2.474 |
|---|---|
| MAD | 9.462 |
| MSD | 135.701 |
주요 결과: MAPE, MAD, MSD
이 결과에서는 세 숫자가 모두 두 번째 모형의 경우 첫 번째 모형보다 낮습니다. 따라서 두 번째 모형의 적합도가 더 높습니다.
3단계: 예측값이 정확한지 여부 확인
예측값이 정확할지 여부를 확인하려면 그림의 적합치 및 예측값을 조사하십시오. 적합치는 특히 계열의 끝에서 데이터를 가깝게 따라야 합니다. 적합치가 계열의 끝에서 데이터로부터 멀어지거나 예측값의 추세선이 데이터의 일반적인 흐름과 일치하지 않으면 기본 추세가 아직 변경 중일 수도 있습니다. 기본 추세의 변화가 단기적인지 또는 장기적인지 확인하려면 더 많은 데이터를 수집해 보십시오.
예측값이 정확해 보이더라도 앞으로 너무 멀리 예측하는 데는 주의해야 합니다. 일반적으로 향후 6기간만 예측해야 합니다.

이 평활 그림에서는 계열의 끝에서 추세가 변화하는 것으로 보입니다. 예측값의 추세선은 데이터의 전체적인 장기 추세만큼 가파르지 않지만, 이러한 차이는 모형이 계열의 끝에서 추세 변화에 따라 수정되기 때문입니다. 예측값은 향후 6개월 간 판매량이 약간 상승할 것으로 예측합니다.
