1단계: 자기 상관 증거 확인
두 계열에서 자기 상관의 증거를 확인하려면 서서히 0으로 감소하는 양쪽의 상관 중에서 큰 상관에 대한 교차 상관 함수를 조사하십시오 일반적으로 자기 상관 때문에 두 시계열 사이에 유의한 관계를 식별하는 데 문제가 발생합니다. 자기 상관의 증거가 있으면 데이터를 미리 백색화해야 합니다. 자세한 내용은 교차 상관 함수를 위한 데이터 사전 백색화에서 확인하십시오.
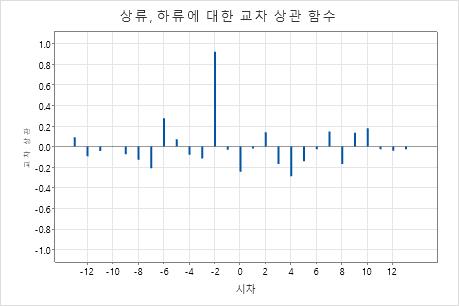
이 그림은 큰 상관이 있지만, 양쪽의 상관이 0으로 서서히 감소하지 않는다는 것을 보여줍니다. 그림은 자기 상관의 증거를 보여주지 않습니다.
2단계: 두 계열 간에 관계가 존재하는지 여부 확인
두 계열 간에 관계가 존재하는지 여부를 확인하려면 양쪽 상관 중에서 신속하게 유의하지 않게 되는 더 큰 상관을 찾으십시오. 일반적으로 절대값이  보다 크면 상관이 유의하며, 여기서 n은 관측치의 수이고 k는 시차입니다. 이 계산은 표본의 정규 근사성을 기반으로 하는 경험 규칙 절차입니다. 시차 k(k = 1,2 ...)의 모집단 교차 상관이 0인 경우 상당히 큰 n에 대해 rxy(k)는 근사적으로 정규 분포를 따릅니다. 이때 평균( m)은 0이고 표준 편차(s)는 (σ) 1/
보다 크면 상관이 유의하며, 여기서 n은 관측치의 수이고 k는 시차입니다. 이 계산은 표본의 정규 근사성을 기반으로 하는 경험 규칙 절차입니다. 시차 k(k = 1,2 ...)의 모집단 교차 상관이 0인 경우 상당히 큰 n에 대해 rxy(k)는 근사적으로 정규 분포를 따릅니다. 이때 평균( m)은 0이고 표준 편차(s)는 (σ) 1/ 입니다. 정규 모집단의 약 95%가 평균의 2 표준 편차 내에 있으므로 |rxy(k) |가 2/
입니다. 정규 모집단의 약 95%가 평균의 2 표준 편차 내에 있으므로 |rxy(k) |가 2/ 보다 큰 경우 시차 k의 모집단 자기 상관이 0이라는 가설을 기각하는 검정은 약 5%의 유의 수준(α)을 가집니다.
보다 큰 경우 시차 k의 모집단 자기 상관이 0이라는 가설을 기각하는 검정은 약 5%의 유의 수준(α)을 가집니다.

이 그림에서 시차 −2에서의 상관 계수는 약 0.92입니다. 0.92 > 0.5547 =  이기 때문에 상관 관계가 유의합니다. 2일 동안 상류에서 하류로 물이 이동한다는 결론을 내릴 수 있습니다.
이기 때문에 상관 관계가 유의합니다. 2일 동안 상류에서 하류로 물이 이동한다는 결론을 내릴 수 있습니다.
