한 분석가가 108개월 동안 항공사 승객 수에 대한 데이터를 수집했습니다. 분석가는 ARIMA 모델을 사용하여 데이터에 대한 예측을 생성하려고 합니다. 시계열 그림에서 분석가는 높은 계절적 피크와 낮은 계절 피크의 차이가 시간이 지남에 따라 커진다는 것을 알 수 있습니다. 이 패턴은 분산이 고정되어 있지 않음을 나타냅니다. 분석가는 Box-Cox 변환을 수행하여 분석가가 ARIMA 모델을 적합시키기 전에 분산을 고정시킵니다.
- 표본 데이터 항공승객.MWX를 엽니다.
- 을 선택합니다.
- 시계열에서 승객 수를 입력합니다.
- 계절 기간에 12을 입력합니다.
- Minitab 통계 소프트웨어가 사용할 변환을 검색하도록 선택합니다 최적 λ .
- 시간 척도를 위한 스탬프 열에서 날짜를 입력합니다.
- 변환된 시계열을 저장할 위치에서 변환를 입력합니다. 확인을 클릭합니다.
결과 해석
방법 테이블에는 분석에 대한 설정과 변환에 대한 λ 값이 표시됩니다.
이 결과에서 계절 기간은 12이고 분석은 기본 범위 -1과 2 사이의 λ 값을 검색합니다. λ의 최적 값은 약 -0.14입니다. 분석은 값을 0으로 반올림하고 자연 로그 변환을 사용합니다.
방법
| 계절 기간 | 12 |
|---|---|
| 간격에서 최적의 λ 선택 | [-1, 2] |
| 최적 λ | -0.144439 |
| 반올림된 최적 λ | 0 |
| 변환된 계열 = ln(승객 수) |
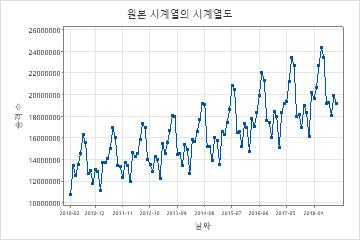
원래 계열의 시계열을 변환된 계열의 시계열 그림과 비교하여 변형으로 인해 분산이 고정되는지 확인합니다.
이 결과에서 원래 계열의 시계열 그림은 고정되지 않은 분산을 보여 줍니다. 이 데이터에서 계절 주기의 높은 지점과 낮은 지점 간의 차이는 시간이 지남에 따라 증가합니다. 이 패턴은 시간이 지남에 따라 분산이 증가한다는 것을 보여줍니다.
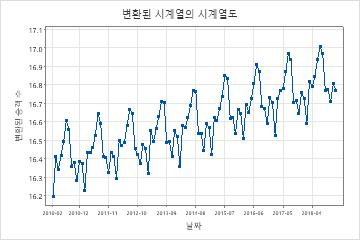
변환된 계열의 시계열 플롯을 검사하여 변환이 분산을 고정시키는지 확인합니다.
이 결과에서 변환된 계열의 시계열 그림은 계절 주기의 높은 점과 낮은 점 간의 거의 균등한 차이를 보여 줍니다. 이 패턴은 변환이 분산을 고정시키는 것을 보여줍니다.
또한 변환된 데이터의 시계열 플롯을 검사하여 변환된 계열의 다른 중요한 특성을 평가합니다. 예를 들어, ARIMA 모델에 대한 가정에는 계열의 고정 분산 외에 고정 평균이 있다는 것이 포함됩니다. 변환된 계열의 시계열 그림에 변환된 계열에 고정 평균이 없음을 보여 주는 경우 데이터를 차이점으로 보관하면 계열의 평균 증대된 Dickey-Fuller 검정 이 고정되는지 확인합니다.
이 결과에서 변환된 계열은 상승 추세를 보여줍니다. 이 패턴은 계열의 평균이 고정되어 있지 않음을 보여줍니다. 증대된 Dickey-Fuller 검정 변환된 데이터의 저장된 열에 있는 것을 사용하여 차이점 보관으로 인해 계열이 고정되는지 확인합니다.