원하는 방법 또는 공식을 선택하십시오.
이 항목의 내용
ACF
ARIMA 잔차의 자기 상관 함수(ACF)에 대한 그래프에는 유의 한계를 나타내는 선이 포함됩니다. 유의 한계를 벗어나는 값은 약 α = 0.05에서 통계적으로 유의하며, 자기 상관이 0이 아니라는 증거를 보여줍니다.
공식
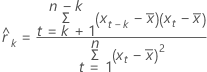
표기법
| 용어 | 설명 |
|---|---|
| k | 시차, k = 1, 2,... |
| xt | t행에서 x의 값 |
 | x의 평균 |
| n | 계열의 관측치 수 |
ACF의 표준 오차
공식
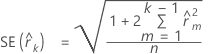
표기법
| 용어 | 설명 |
|---|---|
 |  |
| k | 시차, k = 1, 2, ... |
| n | 계열의 관측치 수 |
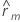 | 시차 m의 자기 상관 |
t-통계량
공식

표기법
| 용어 | 설명 |
|---|---|
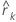 | 시차 k에서의 자기 상관, k = 1, 2, ... |
 | 시차 k에서의 자기 상관의 표준 오차 |
유의 한계
공식
시차 k에서의 상한 = tn−1, 0.975 × SE(rk)
시차 k에서의 하한 = tn−1, 0.025 × SE(rk)
표기법
| 용어 | 설명 |
|---|---|
| SE(rk) | 시차 k에서의 자기 상관의 표준 오차 |
| tn-1, 0.975 | 자유도가 n – 1인 t 분포의 97.5번째 백분위수 |
| tn-1, 0.025 | 자유도가 n – 1인 t 분포의 2.5번째 백분위수 |
Ljung-Box Q 통계량
공식
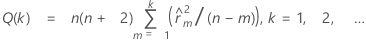
표기법
| 용어 | 설명 |
|---|---|
| n | 계열의 관측치 수 |
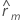 | 시차 m에서 추정된 자기 상관, m = 1, 2, ..., k |
| k | 시차, k = 1, 2, ... |
