방법 표
방법 테이블에는 분석에 대한 설정과 선택한 지연 순서가 표시됩니다.
이 결과에서 분석에서 평가하는 최대 지연 순서는 9입니다. 분석에서는 지연 순서가 가장 높은 모형을 4로 사용하여 테스트 결과를 계산합니다.
방법
| 회귀 모델의 항에 대한 최대 지연 순서 | 9 |
|---|---|
| 지연 순서 선택 기준 | 최소 AIC |
| 추가 항 | 상수 |
| 선택한 지연 순서 | 4 |
| 사용된 행 | 36 |
증강 디키-풀러 테스트 테이블
Augmented Dickey-Fuller 테스트 테이블은 가설, 테스트 통계, p-값 및 시리즈를 고정시키기 위해 차이점 보관을 고려해야 하는지 여부에 대한 권장 사항을 제공합니다.
검정 통계량은 귀무 가설을 평가하는 한 가지 방법을 제공합니다. 임계 값보다 작거나 같은 테스트 통계는 귀무 가설에 대한 증거를 제공합니다.
p-값은 귀무 가설에 반하는 증거를 측정하는 확률입니다. p-값이 작을수록 귀무 가설에 반하는 더 강력한 증거가 됩니다.
데이터를 차이로 구분할지 여부를 결정하려면 검정 통계량을 임계 값과 비교하거나 p-값을 유의 수준과 비교합니다. p-값에 더 많은 근사치가 포함되어 있기 때문에 분석의 권장 사항은 유의 수준이 0.01, 0.05 또는 0.10일 때 임계 값을 사용하여 귀무 가설을 평가합니다. 일반적으로 결론은 임계 값과 p-값에 대해 동일합니다. 귀무 가설은 데이터가 고정되어 있지 않다는 것인데, 이는 차이점 보관이 데이터를 고정시키려는 합리적인 단계임을 의미합니다.
- 유의 수준≤ P-값
- 테스트 통계 ≤ 임계 값
- p-값이 유의 수준보다 작거나 같거나 검정 통계량이 임계 값보다 작거나 같은 경우 귀무 가설을 기각하기로 결정합니다. 데이터가 고정되어 있다는 증거를 제공하기 때문에 분석의 권장 사항은 차이점 보관하지 않고 진행하는 것입니다.
- 유의 수준> P-값
- 테스트 통계 > 임계 값
- p-값이 유의 수준보다 크거나 검정 통계량이 임계 값보다 큰 경우 귀무 가설을 기각하지 않기로 결정합니다. 데이터가 고정되어 있다는 증거를 제공하지 않기 때문에 분석의 권장 사항은 차이점 보관이 데이터의 평균을 고정시키는지 여부를 확인하는 것입니다.
이 결과에서 2.29045의 검정 통계량은 약 -2.96053의 임계 값보다 큽니다. 결과가 데이터가 고정되어 있지 않다는 귀무 가설을 기각하지 못하기 때문에 테스트의 권장 사항은 데이터를 고정시키기 위해 차이점 보관을 고려하는 것입니다.
증대된 Dickey-Fuller 검정
| 귀무 가설: | 데이터는 고정되지 않습니다. |
|---|---|
| 대립 가설: | 데이터는 고정되어 있습니다. |
| 검정 통계량 | P-값 | 추천 |
|---|---|---|
| 2.29045 | 0.999 | 검정 통계 > -2.96053의 임계값. |
| 유의 수준 = 0.05 | ||
| 귀무 가설을 거부하지 않습니다. | ||
| 데이터를 고정하기 위해 차분 계산을 고려하십시오. |
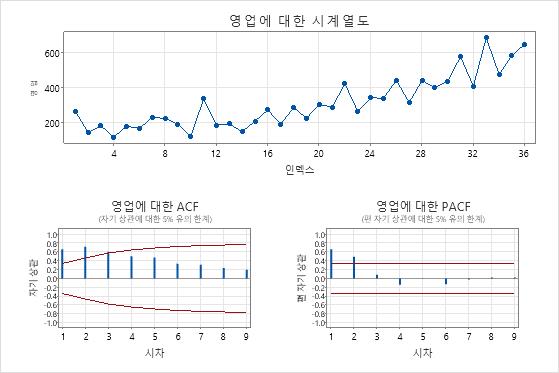
오리지널 시리즈의 플롯
- 시계열도
- 원본 계열의 시계열 그림을 사용하여 원본 데이터의 특성을 검사합니다. 추세는 고정되지 않은 평균을 나타내는 패턴의 예입니다. 차이점 보관을 사용하여 평균을 고정되도록 합니다.
- ACF 그림
- 원본 데이터의 ACF(자기 상관 함수)를 사용하여 데이터의 평균이 고정되어 있지 않음을 나타내는 패턴을 찾습니다. 일반적인 패턴은 매우 느리게 사라지는 지연에 걸친 큰 스파이크입니다.
- PACF 그림
- 일반적으로 고정 데이터의 부분 자기 상관 함수(PACF)를 사용하여 ARIMA 모델에서 자기회귀 항의 존재를 나타내는 패턴을 찾습니다. 원본 데이터가 고정되어 있지 않은 경우 차이 계열의 PACF 플롯을 사용하여 ARIMA 모델의 후보 항을 찾습니다.
이 결과에서 데이터는 시계열 그림의 증가 추세를 보여줍니다. ACF 플롯의 첫 번째 지연은 5% 유의 한도를 초과하는 큰 스파이크를 표시한 다음 매우 느리게 감소합니다. 이러한 패턴은 데이터의 평균이 고정되어 있지 않음을 나타냅니다.
판매는 결정론적 추세를 설명하는 예측 변수와 관계가 없고 분석가가 ARIMA 모델을 사용하여 판매를 예측하려고 하기 때문에 데이터를 다르게 보관하는 것은 계열의 평균을 고정시키는 합리적인 방법입니다.
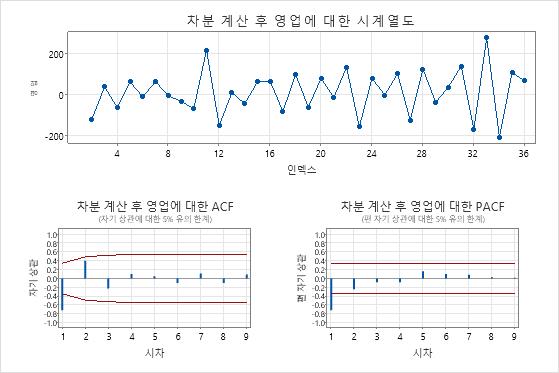
차이 시리즈의 플롯
- 차이점 보관 후의 시계열 그림
- 차이 데이터의 시계열 그림을 사용하여 차이점 보관이 데이터의 평균을 고정시키는지 확인합니다. 시계열 그림은 연속 관측치 간의 차이를 보여 줍니다. 고정 평균이 있는 데이터는 시계열 그림의 수평 경로를 따릅니다.
- 차이점 보관 후 ACF 플롯 및 PACF 플롯
- 차이 있는 데이터의 ACF를 사용하여 차이점 보관이 데이터의 평균을 고정시키는지 확인합니다. 빠르게 감소하는 스파이크가있는 플롯은 고정 된 데이터의 특징입니다.
이 결과에서 시계열 그림은 차이 데이터의 평균과 분산이 거의 일정하다는 것을 보여줍니다. 데이터가 고정되어 있는 것처럼 보입니다.
차이 데이터의 ACF 플롯에서 0과 유의하게 다른 스파이크는 지연 1에 있습니다. 이 패턴은 또한 데이터가 고정되어 있음을 나타냅니다.