원하는 방법 또는 공식을 선택하십시오.
이 항목의 내용
계수
후방 예측값
후방 예측값은 지정된 모형 및 현재 반복의 모수 추정치를 사용하여 계산됩니다. 자세한 내용은 Cryer3를 참조하십시오.
SSE
공식

표기법
| 용어 | 설명 |
|---|---|
| n | 총 관측치 수 |
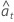 | 반복의 모수 추정치를 사용하는 잔차(후방 예측값 포함) |
잔차에 대한 SS
공식
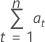
표기법
| 용어 | 설명 |
|---|---|
| n | 총 관측치 수 |
| at | 마지막 모수 추정치를 사용하는 잔차(후방 예측값 제외) |
잔차에 대한 DF
공식
상수 항이 있는 모형의 경우:
(n – d) – p – q – 1
상수 항이 없는 모형의 경우:
(n – d) – p – q
표기법
| 용어 | 설명 |
|---|---|
| n | 총 관측치 수 |
| d | 차이의 수 |
| p | 모형에 포함된 자기회귀 모수의 수 |
| q | 모형에 포함된 이동 평균[MA] 모수의 수 |
잔차에 대한 MS
공식
SS / DF
카이-제곱 통계량
공식
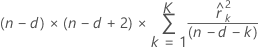
표기법
| 용어 | 설명 |
|---|---|
| n | 총 관측치 수 |
| d | 차이의 수 |
| K | 12, 24, 36, 48 |
| k | 시차 |
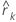 | k번째 시차에 대한 잔차의 자기 상관 |
카이-제곱 통계량에 대한 DF
공식
상수 항이 있는 모형의 경우:
K – p – q – 1
상수 항이 없는 모형의 경우:
K – p – q
표기법
| 용어 | 설명 |
|---|---|
| K | 12, 24, 36, 48 |
| p | 모형에 포함된 자기회귀 모수의 수 |
| q | 모형에 포함된 이동 평균[MA] 모수의 수 |
카이-제곱 통계량에 대한 p-값
공식
P(X < χ2)
표기법
| 용어 | 설명 |
|---|---|
| X | χ2(DF)으로 분포됨 |
예측값
수식
예측값은 모형 및 모수 추정치를 기반으로 반복적으로 계산됩니다. 예를 들어, ARIMA 모형이 1개의 자기회귀 항(AR(1)) 및 계절 기간이 12인 하나의 계절적 차분 계산 항으로 적합되면 다음 모형이 적합합니다.
Yt – Yt–12 = γ + Φ(Yt–1 – Yt–12-1)
첫 번째 예측값  을 추정하려면(여기서 k는 시점)
을 추정하려면(여기서 k는 시점)
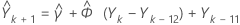
을 찾습니다. 동일한 방식으로 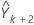 를 찾고 이런 식으로 계속합니다.
를 찾고 이런 식으로 계속합니다.
예측에 대한 95% 예측 구간을 계산하려면 먼저 가중치를 계산해야 합니다.
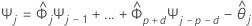
설명 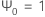 ,
,  j < 0의 경우,
j < 0의 경우,  j > q의 경우.
j > q의 경우.
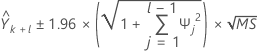
표기법
| 용어 | 설명 |
|---|---|
| Yt | 시간 t에서의 실제 값 |
| Φ | 자기회귀 항 |
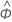 | 추정된 자기회귀 항 |
| γ | 상수 항 |
| d | 차이의 수 |
| p | 자기회귀 모수의 수 |
| q | 이동 평균 모수의 수 |
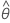 | 추정된 이동 평균 항 |
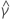 | 추정된 상수 항 |
| MS | 평균 제곱 오차 |
1 G.E.P. Box and G.M. Jenkins (1994). Time Series Analysis: Forecasting and Control, 3rd Edition. Prentice Hall
2 W. Q. Meeker (1978). "TSERIES-A User-Oriented Computer Program for Time Series Analysis", The American Statistician, 32, 111-112.
3 J.D. Cryer (1986). Time Series Analysis. Duxbury Press
