Weibull 분포를 사용하여 신뢰도 데이터 모형화
- 초기 고장 기간 동안 몇 퍼센트의 품목에 고장이 발생할 것으로 예상되는가? 예를 들어, 초기 고장 기간인 8시간 동안 몇 퍼센트의 퓨즈에 고장이 발생할 것으로 예상되는가?
- 실제 사용 수명 단계 동안 몇 개의 보증 클레임을 예상할 수 있는가? 예를 들어, 이 타이어의 실제 사용 수명 기간인 50,000마일 동안 몇 개의 보증 클레임을 받을 것으로 예상되는가?
- 언제 빠른 마모가 발생할 것으로 예상되는가? 예를 들어, 엔진이 마모 단계에 들어가지 않도록 하려면 언제 유지보수의 정기적인 일정을 결정해야 하는가?
Weibull 분포는 오른쪽으로 치우치거나, 왼쪽으로 치우치거나 대칭적인 데이터를 모형화할 수 있습니다. 따라서 이 분포는 진공관, 축전기, 볼베어링, 릴레이, 자재 강도 등 다양한 분야에 걸쳐 신뢰도를 평가하기 위해 사용됩니다. Weibull 분포는 또한 감소하거나 증가하거나 일정한 위험 함수를 모형화하여 품목의 수명 단계를 설명할 수 있습니다.
제품 고장이 반도체 고장과 함께 발생할 수 있는 부식과 같이 화학 반응 또는 저하 과정에 의해 야기되는 경우에는 Weibull 분포가 효과적으로 작동하지 않을 수도 있습니다. 일반적으로 이러한 상황은 로그 정규 분포를 사용하여 모형화됩니다.
- Rayleigh 분포
- 형상 모수가 2인 Weibull 분포는 Rayleigh 분포로 알려져 있습니다. 이 분포는 입력 리턴 손실 측정값, 모듈레이션 사이드 밴드 인젝션, 캐리어 서프레션, RF 페이딩 등 커뮤니케이션 엔지니어링 분야의 측정 데이터를 설명하기 위해 주로 사용됩니다. 이 분포는 또한 전자 진공 장치의 수명 검사에 일반적으로 사용됩니다.
- 가장 약한 연결 모형
- Weibull 분포는 또한 중요한 단계에 도달하는 첫 번째 공정에 따라 고장 시간이 결정되는, 고장으로 이어지는 동일하고 독립적인 공정이 많은 수명 분포를 모형화할 수 있습니다. 여러 결점이 궁극적인 고장 장소의 후보가 되는 이러한 '가장 약한 연결' 모형의 기반은 극단값 이론입니다. Weibull 분포는 이론적으로 가장 작은 극단값 분포에서 파생될 수 있기 때문에 축전기, 볼베어링, 릴레이, 재료 강도 고장 등 가장 약한 연결 분야에 대한 효과적인 모형을 제공할 수도 있습니다. 그러나 Weibull 분포는 하한이 0이어서 양수 값만 모형화할 수 있기 때문에 관심 변수가 음수 값을 가질 수 있는 경우에는 가장 작은 극단값 분포가 더 낫습니다.
예 1: 축전기
고장 데이터(시간)를 얻기 위해 높은 스트레스 조건에서 축전기를 검사했습니다. 고장 데이터는 Weibull 분포에 의해 모형화되었습니다.
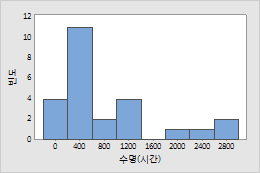
예 2: 필라멘트
한 전구 회사에서 정상 사용 시 장기간 마모되지 않을 것으로 예상되는 백열 필라멘트를 제조합니다. 이 회사의 엔지니어는 전구 수명을 10년으로 보장하려고 합니다. 엔지니어들은 장기간 사용을 시뮬레이션하기 위해 전구에 스트레스를 가하고 각 전구에 고장이 발생할 때까지의 시간을 기록합니다.
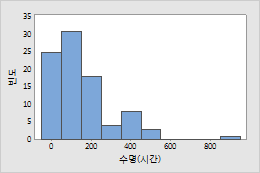
Weibull 분포 모수, 신뢰도 함수, 위험 함수의 관계
Weibull 분포의 형상 모수 β를 조정하여 많은 수명 분포의 특성을 모형화할 수 있습니다.
0 < ß < 1
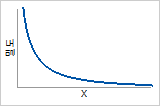
확률밀도함수
무한대에서 기하급수적으로 감소
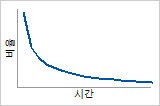
위험 함수
초기의 높은 고장률이 시간이 지남에 따라 감소(“욕조” 모양 위험 함수의 첫 번째 부분)
ß = 1
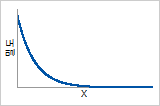
확률밀도함수
1/α에서 기하급수적으로 감소(α = 척도 모수)

위험 함수
제품 수명 기간 동안 고장률이 일정함(“욕조” 모양 위험 함수의 두 번째 부분)
ß = 1.5
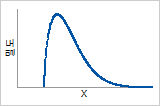
확률밀도함수
최대값까지 증가한 다음 감소
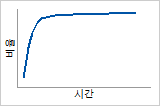
위험 함수
고장률 증가(초기에 가장 크게 증가)
ß = 2
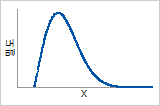
확률밀도함수
Rayleigh 분포
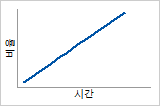
위험 함수
고장률이 선형으로 증가
3 ≤ ß ≤4
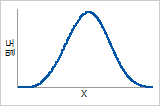
확률밀도함수
종 모양
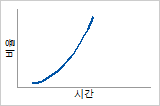
위험 함수
빠르게 증가
ß > 10
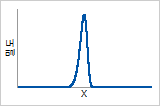
확률밀도함수
극단값 분포와 유사함
위험 함수
매우 빠르게 증가
