로그 정규 분포를 사용하여 신뢰도 데이터 모형화
로그 정규 분포는 정규 분포와 밀접하게 관련되어 있는 유연한 분포입니다. 이 분포는 대략 대칭이거나 오른쪽으로 치우친 데이터를 모형화하는 데 특히 유용합니다. Weibull 분포와 마찬가지로, 로그 정규 분포는 척도 모수에 따라 모양이 크게 다를 수 있습니다.
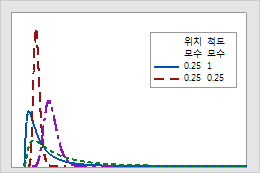
실제로 로그 정규 모형 및 Weibull 모형이 특정 수명 검사 데이터를 동일하게 잘 적합시킬 수도 있습니다. 그러나 반드시 고려해야 할 중요한 차이가 하나 있습니다. 이러한 분포를 사용하여 표본 데이터의 범위를 넘어 추정하는 경우에는 로그 정규 분포가 Weibull 분포보다 초기의 평균 고장률을 더 낮게 예측합니다.
로그 정규 분포는 많은 하이테크 분야에서 가장 일반적으로 사용되는 수명 분포 모형으로 불려 왔습니다. 이 모형은 승법 성장 모형을 기반으로 하며, 이는 공정의 저하 비율이 항상 현재 상태에 비례하여 랜덤하게 증가한다는 것을 의미합니다. 이러한 모든 랜덤 독립 성장의 승법 효과가 누적되어 고장을 유발합니다. 따라서 이 분포는 보통 다음과 같은 분야를 포함하여 주로 스트레스나 피로로 인해 고장나는 부품을 모형화하는 데 사용됩니다.
- 부식, 전이 또는 발산 등 반도체 고장에 일반적인 화학 반응 또는 저하로 인한 고장
- 피로 균열의 증가에 따라 금속이 갈라지는 시간
- 특정 시간이 지나면 고장 위험이 감소하는 전자 부품
예 1: 전자 부품
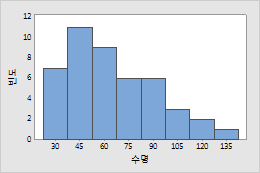
엔지니어들이 정상 작동 조건에서 전자 부품의 수명을 기록합니다. 부품의 고장 위험은 시간이 경과함에 따라 감소하므로, 로그 정규 분포를 사용하여 모형화할 수 있습니다.
예 2: 디젤 발전기 팬
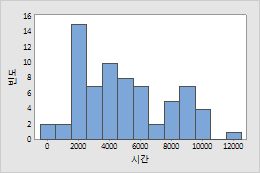
디젤 발전기 팬의 수명 기간 동안 고장 발생 시간을 추적했습니다. 데이터를 모형화하기 위해 로그 정규 분포가 사용되었습니다.
로그 정규 분포에 대한 확률밀도함수 및 위험 함수
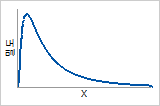
확률밀도함수
데이터가 오른쪽으로 치우쳐 있습니다.
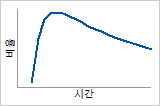
위험 함수
고장 위험이 최대값까지 증가한 다음 감소합니다.
