위험 함수는 지정된 시간에서의 순간 고장률입니다. 위험 함수의 특성은 특정 제품 및 분야와 빈번하게 연관됩니다. 여러 분포 모형을 사용하여 여러 위험 함수가 모형화됩니다. 위험 함수를 비모수 방식으로 모형화할 수도 있습니다.
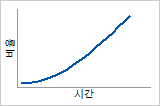
- 증가하는 위험 함수
-
시간이 지남에 따라 품목이 고장날 확률이 높다는 것을 나타냅니다. 예를 들어, 스트레스를 받거나 피로해지기 쉬운 많은 기계적 품목은 제품의 수명이 경과함에 따라 고장의 위험이 증가합니다. 엔지니어는 검사를 사용하여 마모 스트레스를 시뮬레이션할 수도 있습니다. 예를 들어, 엔지니어는 전구의 장기적인 사용을 시뮬레이션한 다음 고장이 발생할 때까지의 시간을 기록합니다.
이러한 유형의 마모 고장을 모형화하는 데는 Weibull 분포가 흔히 사용됩니다.
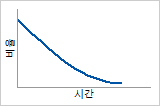
- 감소하는 위험 함수
-
제품 수명의 초기 단계에서 고장이 발생할 확률이 높다는 것을 나타냅니다. 한 가지 예는 사용하면 경화되어 시간이 지남에 따라 더 강해지는 금속으로 구성된 제품 또는 부품입니다. 또는 새 소프트웨어 프로그램을 출시할 때가 되면 발생할 확률이 높지만 시간이 지남에 따라 감소하는 컴퓨터 프로그램의 오류입니다.
이러한 유형의 데이터는 흔히 형상 모수가 1보다 작은 Weibull 분포를 사용하여 모형화할 수 있습니다.
- 일정한 위험 함수
-
제품 수명의 모든 단계에서 고장이 발생할 확률이 동일하다는 것을 나타냅니다. 고장 위험이 상대적으로 일정한 이 패턴은 욕조 곡선의 중간 부분의 특성입니다.
이 함수는 지수 분포를 사용하여 모형화할 수 있습니다.

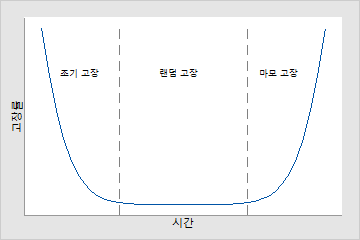
- 욕조 모양 위험 함수
-
많은 제품의 고장률 분포는 "욕조" 모양의 곡선을 따릅니다. 위험률은 종종 초기에는 높고, 중기에는 낮으며, 말기에는 다시 높습니다. 따라서 이러한 세 가지 고장 기간의 결과 곡선은 욕조 모양과 비슷해집니다. 텔레비전과 휴대용 계산기가 일반적으로 욕조 모양 위험 함수를 보여주는 두 가지 제품입니다. 또한 마이크로프로세서는 컴퓨터 시스템에 설치한 직후 고장이 발생할 수 있습니다.
Minitab을 사용하여 욕조 함수에서 지정된 기간을 모형화할 수 있습니다. Minitab은 감소하는 위험, 일정한 위험 또는 증가하는 위험을 모형화하지만 제품 수명의 세 가지 기간을 모두 순차적으로 모형화하지는 못합니다.