엔지니어들이 재설계된 압축기 덮개의 신뢰도를 평가하려고 합니다. 엔지니어들은 설계를 검사하기 위해 기계를 사용하여 각 압축기 덮개로 단일 투사체를 던집니다. 그런 다음 투사체가 충격을 가한 후 12시간마다 압축기에 고장이 발생했는지 검사합니다.
엔지니어들은 덮개 설계, 투사체 무게 및 고장 시간 간의 관계를 평가하기 위해 수명 데이터 회귀 분석을 수행합니다. 또한 엔진의 1% 및 5%가 고장날 것이라고 예상할 수 있는 고장 시간을 추정하려고 합니다. 엔지니어들은 Weibull 분포를 사용하여 데이터를 모형화합니다.
- 표본 데이터제트엔진신뢰도.MWX을 엽니다.
- 을 선택합니다.
- 반응이 비 관측 중단/임의 관측 중단 데이터임을 선택합니다.
- 변수/시작 변수에 시작을 입력합니다.
- 끝 변수에 끝을 입력합니다.
- 모형에 설계 및 무게을 입력합니다.
- 요인(옵션)에 설계을 입력합니다.
- 추정치을 클릭합니다. 새 예측 변수 값 입력에 새 설계새 무게을 입력합니다.
- 백분율에 대한 백분위수 추정에 1 5를 입력한 다음 확인을 클릭합니다.
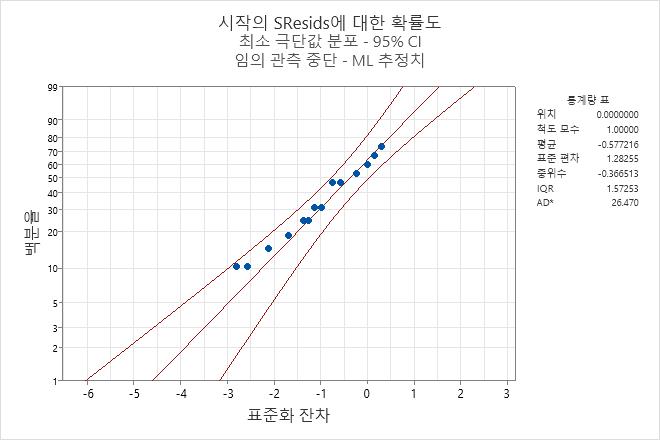
- 그래프을 클릭합니다. 표준화 잔차에 대한 확률도을 선택합니다.
- 각 대화 상자에서 확인을 클릭합니다.
결과 해석
회귀 분석 표에서는 설계 및 무게에 대한 p-값이 0.05의 α-수준에서 유의합니다. 따라서 엔지니어는 덮개 설계와 투사체 무게 모두 수명에 통계적으로 유의한 영향을 미친다는 결론을 내립니다. 예측 변수에 대한 계수는 덮개 설계, 투사체 무게, 엔진의 수명 간 관계를 설명하는 방정식을 정의하기 의해 사용할 수 있습니다.
백분위수 표에는 덮개 설계와 투사체 무게의 각 조합에 대한 첫 번째와 5번째 백분위수가 표시됩니다. 새 덮개 설계의 경우 엔진의 1% 또는 5%가 고장나는 데 걸리는 시간이 모든 투사체 무게에서 표준 설계보다 더 깁니다. 예를 들어, 10파운드 투사체를 적용한 후 표준 덮개 설계를 사용한 엔진의 1%가 약 101.663시간 후 고장날 것으로 예상할 수 있습니다. 새 덮개 설계를 사용하면 엔진의 1%가 약 205.882시간 후 고장날 것으로 예상됩니다.
표준화 잔차의 확률도는 점들이 거의 직선을 따른다는 것을 보여줍니다. 따라서 엔지니어는 모형이 적절하다고 가정할 수 있습니다.
관측 중단
| 관측 중단 정보 | 카운트 |
|---|---|
| 우측 관측 중단 값 | 25 |
| 구간 관측 중단 값 | 23 |
회귀 분석 표
| 95.0% 정규 CI | ||||||
|---|---|---|---|---|---|---|
| 예측 변수 | 계수 | 표준 오차 | Z | P | 하한 | 상한 |
| 절편 | 6.68731 | 0.193766 | 34.51 | 0.000 | 6.30754 | 7.06709 |
| 설계 | ||||||
| 표준 | -0.705643 | 0.0725597 | -9.72 | 0.000 | -0.847857 | -0.563428 |
| 무게 | -0.0565899 | 0.0212396 | -2.66 | 0.008 | -0.0982187 | -0.0149611 |
| 형상 모수 | 5.79286 | 1.07980 | 4.02001 | 8.34755 | ||
Anderson-Darling(수정) 적합도
백분위수 표
| 95.0% 정규 CI | ||||||
|---|---|---|---|---|---|---|
| 백분율 | 설계 | 무게 | 백분위수 | 표준 오차 | 하한 | 상한 |
| 1 | 표준 | 5.0 | 134.911 | 17.6574 | 104.385 | 174.363 |
| 1 | 표준 | 7.5 | 117.113 | 16.0279 | 89.5591 | 153.144 |
| 1 | 표준 | 10.0 | 101.663 | 16.3830 | 74.1295 | 139.423 |
| 1 | 새 브랜드 | 5.0 | 273.214 | 36.8022 | 209.819 | 355.763 |
| 1 | 새 브랜드 | 7.5 | 237.171 | 32.6878 | 181.028 | 310.726 |
| 1 | 새 브랜드 | 10.0 | 205.882 | 32.8675 | 150.568 | 281.518 |
| 5 | 표준 | 5.0 | 178.749 | 16.9676 | 148.404 | 215.300 |
| 5 | 표준 | 7.5 | 155.168 | 14.1107 | 129.836 | 185.443 |
| 5 | 표준 | 10.0 | 134.698 | 15.4568 | 107.568 | 168.670 |
| 5 | 새 브랜드 | 5.0 | 361.994 | 36.0778 | 297.761 | 440.084 |
| 5 | 새 브랜드 | 7.5 | 314.239 | 28.8741 | 262.450 | 376.247 |
| 5 | 새 브랜드 | 10.0 | 272.783 | 30.6102 | 218.928 | 339.887 |