주어진 백분율에 대한 백분위수의 포인트 추정치
p번째 백분위수 점 xp는 반응 p에 필요한 응력 수준입니다.
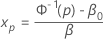
xp의 추정치를 구하려면 다음 공식을 사용하십시오.
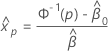
설명 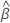 및
및 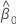 는 최대우도 추정치입니다.
는 최대우도 추정치입니다.  및
및 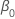 .
.
프로빗 분석에 대한 로그 위치 분포는 로그 정규 분포, 로그 로지스틱 분포 및 Weibull 분포입니다. 로그 위치 분포의 경우 이전 공식은 로그 척도에서 백분위수를 추정합니다. 이러한 분포가 있는 데이터의 척도에서 백분위수를 추정하려면 다음 공식을 사용하십시오.
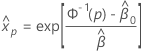
주어진 퍼센트에 대한 백분위수의 표준 오차
백분위수의 표준 오차 계산은 델타 방법을 사용합니다. 추정된 백분위수의 표준 오차에는 다음과 같은 공식이 있습니다.

여기서 의 분산  의 형식은 다음과 같습니다.
의 형식은 다음과 같습니다.
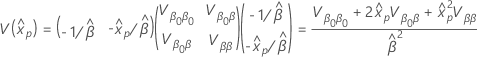
그리고 의 분산-공분산 행렬 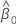 및
및 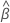 의 형식은 다음과 같습니다.
의 형식은 다음과 같습니다.
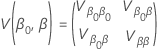
프로빗 분석에 대한 로그 위치 분포는 로그 정규 분포, 로그 로지스틱 분포 및 Weibull 분포입니다. 로그-위치 분포의 경우, 이전 공식은 다음의 분산을 추정합니다. 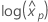 . 분산(variance)과 분산-공분산 행렬(variance-covariance matrix)의 정의(영어)
. 분산(variance)과 분산-공분산 행렬(variance-covariance matrix)의 정의(영어) 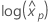 뒤따르다.
뒤따르다.
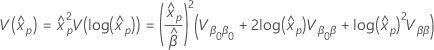

주어진 퍼센트에 대한 백분위수의 기준 신뢰 구간
양측, 100(1 -  )의 경우
)의 경우  다음과 같음
다음과 같음 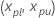 다음 방정식으로.
다음 방정식으로.
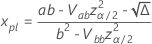
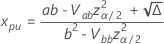
설명
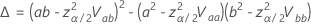
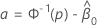

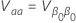


프로빗 분석에 대한 로그 위치 분포는 로그 정규 분포, 로그 로지스틱 분포 및 Weibull 분포입니다. 로그 위치 분포의 경우 이전 공식은 로그 척도의 구간을 추정합니다. 데이터 척도에서 구간을 추정하려면 이전 공식의 신뢰 한계를 지수화하십시오.
주어진 응력 값에서 고장 확률 또는 생존 확률의 기준 신뢰 구간
양측, 100(1 -  )의 실패 확률에 대해,
)의 실패 확률에 대해, 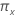 이고, 다음과 같습니다.
이고, 다음과 같습니다.  . 생존 확률에 대해,
. 생존 확률에 대해,  , 간격은 다음과 같습니다.
, 간격은 다음과 같습니다. 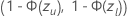 . 다음 수식은 계산을 제공합니다.
. 다음 수식은 계산을 제공합니다.
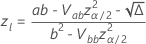
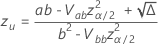
설명
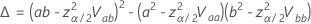


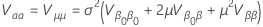

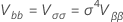
및 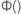 은 분석을 위한 분포의 누적 분포 함수입니다.
은 분석을 위한 분포의 누적 분포 함수입니다.
프로빗 분석에 대한 로그 위치 분포는 로그 정규 분포, 로그 로지스틱 분포 및 Weibull 분포입니다. 로그 위치 분포의 경우 다음 정의를 대체하십시오.

참고 문헌
기준 신뢰 구간의 유도는 Fieller의 정리를 사용합니다. Fieller의 정리는 다음 참조에 있습니다.
Finney, D. J. (1971). Probit analysis, (Third edition), London: Cambridge University Press.
프로빗 모델 및 백분위수 추정에 대한 자세한 내용은 다음 참조를 참조하십시오.
Cox, D. R. and Snell, E. J. (1989). The analysis of binary data (Second edition), London: Chapman & Hall.
