한 신뢰성 공학 엔지니어가 상용 제트기에 사용되는 특정 공기 조절 장치의 고장률을 평가합니다. 이 엔지니어는 비행기 13대의 공기 조절 장치의 고장 데이터를 수집합니다. 해당 장치가 고장날 때마다 수리한 다음 다시 사용했습니다.
엔지니어는 시간이 지남에 따라 고장률이 증가하는지, 감소하는지 또는 일정하게 유지되는지 확인하려고 합니다. 이 데이터의 경우 더 이상 사용되지 않는 공기 조절 장치가 없습니다. 모든 데이터가 정확한 고장 시간입니다.
- 표본 데이터에어컨신뢰성.MWX을 엽니다.
- 을 선택합니다.
- 데이터가 정확한 고장/은퇴 시간임을 선택합니다.
- 변수/시작 변수에 고장을 입력합니다.
- 시스템 ID(옵션)에 시스템을 입력합니다.
- 확인을 클릭합니다.
결과 해석
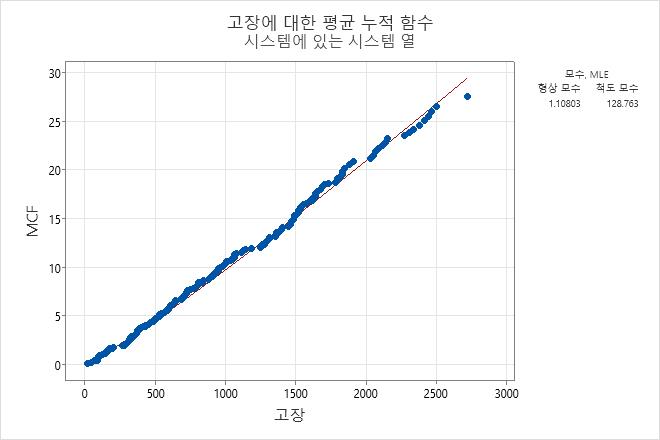
형상 모수의 추정치(1.10803)가 1에 가까우며, 이는 고장률이 시간이 지남에 따라 거의 일정하다는 것을 나타냅니다. 엔지니어는 구간(0.984256, 1.24738)에 모집단에 대한 분포의 실제 형상이 포함된다고 95% 확신할 수 있습니다.
동일 형상 모수에 대한 검정에서는 시스템이 서로 다른 형상 모수를 가진 모집단에서 추출되었다는 결론을 내릴 수 있는 충분한 근거가 없음을 알 수 있습니다(P-값 = 0.539). 따라서 엔지니어는 형상 모수에 대한 합동 추정치가 적절하다고 가정할 수 있습니다.
0.05의 α-수준에서 추세에 대한 어느 검정도 유의하지 않습니다(P-값 = 0.107; P-값 = 0.448, P-값 = 0.388; P-값 = 0.688, P-값 = 0.389). 따라서 엔지니어가 귀무 가설을 기각하고 추세가 존재한다는 결론을 내릴 수 있는 충분한 증거가 없습니다.
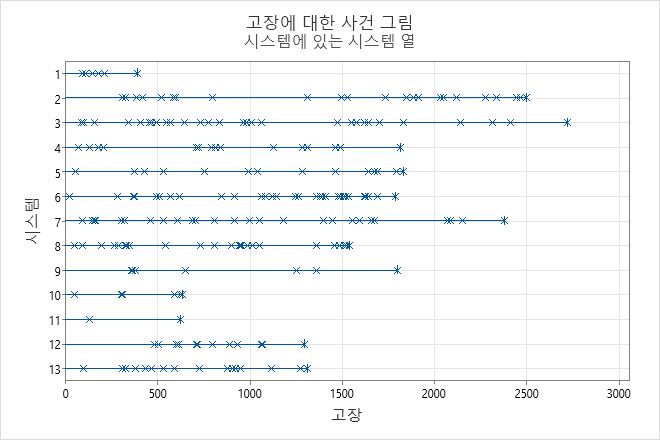
사건 그림이 감소 또는 증가 추세를 보여주지 않습니다. 고장 사이의 시간이 일정한 것으로 보입니다.
고장에 대한 평균 누적 함수의 그림은 선형 관계를 보여주며, 시스템 고장률이 상대적으로 일정하다는 것을 나타냅니다.
모수 추정치
| 95% 정규 CI | ||||
|---|---|---|---|---|
| 모수 | 추정치 | 표준 오차 | 하한 | 상한 |
| 형상 모수 | 1.10803 | 0.067 | 0.984256 | 1.24738 |
| 척도 모수 | 128.763 | 22.489 | 91.4369 | 181.325 |
동일 형상 모수에 대한 검정
| 검정 통계량 | 10.88 |
|---|---|
| P-값 | 0.539 |
| DF | 12 |
추세 검정
| MIL-Hdbk-189 | Laplace의 | ||||
|---|---|---|---|---|---|
| TTT 기반 | 합동 | TTT 기반 | 합동 | Anderson-Darling | |
| 검정 통계량 | 378.17 | 378.28 | 0.86 | -0.40 | 0.94 |
| P-값 | 0.107 | 0.448 | 0.388 | 0.688 | 0.389 |
| DF | 424 | 400 | |||