모수 추정치
공식
| 분포 | 모수 |
|---|---|
|
최소 극단값 분포 정규 분포 로지스틱 분포 |
μ = 위치, σ = 척도, σ > 0 |
|
대수 정규 분포 로그 로지스틱 분포 |
μ = 위치, μ > 0 σ = 척도, σ > 0 |
|
3-모수 로그 정규 분포 3-모수 로그 로지스틱 분포 |
μ = 위치, μ > 0 σ = 척도, σ > 0 λ = 분계점. |
|
Weibull 분포 |
α = 척도, α = exp(μ) β = 형상, β = 1/σ |
|
3-모수 Weibull 분포 |
α = 척도, α = exp(μ) β = 형상, β = 1/σ λ = 분계점, |
|
지수 분포 |
θ = 척도, θ > 0 |
|
2-모수 지수 분포 |
θ = 척도, θ > 0 λ = 분계점, |
모수 추정치의 표준 오차
표준 오차는 모수의 추정치에 대한 표준 편차입니다. 표준 오차는 각 추정치의 변동 측도를 제공합니다.
, 
, 
, 
, 
및 
은 μ, σ, α, β, θ 및 λ의 MLE 표준 오차를 나타냅니다. 각 표준 오차는 Fisher 정보 행렬에 대한 역의 적절한 대각 원소의 제곱근으로 계산됩니다.
모수 추정치에 대한 신뢰 한계
공식
| 분포 | 모수 | 신뢰 하한 | 신뢰 상한 |
|---|---|---|---|
| 최소 극단값 분포, 정규 분포, 로지스틱 분포, 로그 정규 분포, 로그 로지스틱 분포 | 위치, μ |
 |
 |
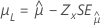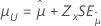| 척도, σ |
 |
 |
|
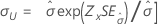| 3-모수 로그 정규 분포, 3-모수 로그 로지스틱 분포 | 위치, μ |
 |
 |
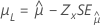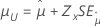| 척도, σ |
 |
 |
|
| 분계점, λ |
 |
 |
|
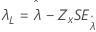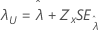| Weibull 분포 | 형상, β |
 |
 |
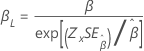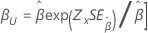| 척도, α |
 |
 |
|
|
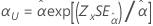3-모수 Weibull 분포 |
형상, β |
 |
 |
|
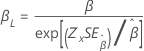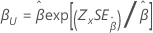척도, α |
 |
 |
|
|
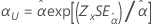분계점, λ |
 |
 |
|
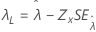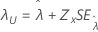| 지수 분포 | 척도 |
 |
 |
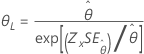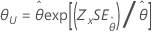| 2-모수 지수 분포 | 척도, θ |
 |
 |
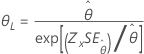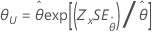| 분계점, λ |
 |
 |
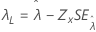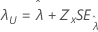참고
일부 데이터의 경우 우도 함수의 경계가 없으므로 분계점 모수가 있는 분포(예: 2-모수 지수 분포)에 대한 일관성이 없는 추정치가 산출됩니다. 이러한 일이 발생하는 경우, 추정된 모수의 분산-공분산 행렬을 숫자상으로 확인할 수 있습니다. 이 경우 Minitab에서는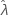 
가 고정되었다고 가정하며 SE (
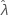) = 0이라는 결과가 나옵니다. 
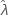에 대한 상한 및 하한은 
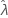입니다.
표기법
| 용어 | 설명 |
|---|---|
| zx | 표준 정규 분포에 대한 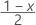 상위 임계값, 여기서 100x %는 신뢰 수준이고 0 < x < 1입니다. |
모수 추정값에 대한 로그 우도
다양한 중도절단 체계에 대한 우도 함수는 Meeker et al.에 있습니다. (2022)1.
