이 항목의 내용
확률도
선택한 분포가 데이터를 얼마나 잘 적합하는지 평가하려면 확률도를 사용합니다. 점들이 적합선을 가까이 따르면 분포가 데이터를 상당히 잘 적합한다고 가정할 수 있습니다.
- 그림 위의 점은 (어떠한 분포에도 의존하지 않는) 비모수 방법에 바탕을 둔 추정 백분위수입니다. 데이터 점에 포인터를 놓으면 관측된 수명과 추정된 누적 확률이 표시됩니다.
- 적합선(중심선)은 적합된 분포에 바탕을 두고 있습니다. 적합선 위에 포인터를 놓으면 다양한 백분율에 대한 백분위수 표가 표시됩니다.
- 왼쪽 선은 각 백분위수에 대한 신뢰 구간의 하한을 연결합니다. 오른쪽 선은 각 백분위수에 대한 신뢰 구간의 상한을 연결합니다.
출력 예
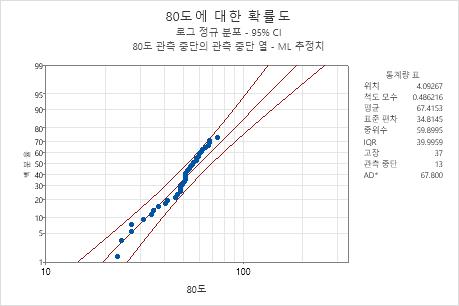
해석
엔진 와인딩 데이터의 80도 표본의 경우, 점들이 적합선을 따르는 것으로 보입니다. 따라서 로그 정규 분포가 데이터에 대한 적절한 선택이라고 가정할 수 있습니다. 적합선은 위치 모수 = 4.09267이고 척도 모수 = 0.486216인 로그 정규 분포에 바탕을 두고 있습니다.
생존 그림
생존 그림은 항목이 특정 시간까지 생존할 확률을 나타냅니다. 따라서 생존 그림은 시간 경과에 따른 제품의 신뢰도를 표시합니다.
- 중심선은 시간 경과에 따른 추정된 신뢰도입니다.
- 오른쪽 선은 각 시점에서 신뢰도에 대한 상한을 연결한 것입니다. 왼쪽 선은 각 시점에서 신뢰도에 대한 하한을 연결한 것입니다.
생존 곡선 위에 포인터를 놓으면 수명과 생존 확률의 표가 표시됩니다.
이 그림은 분포가 데이터를 잘 적합시킨 경우에만 사용해야 합니다. 선택된 분포가 데이터를 잘 적합하지 않으면 이러한 추정치가 부정확하게 됩니다. 분포가 데이터를 잘 적합하는지 여부를 확인하려면 분포 ID 그림, 확률도 및 적합도 측도를 사용합니다.
출력 예
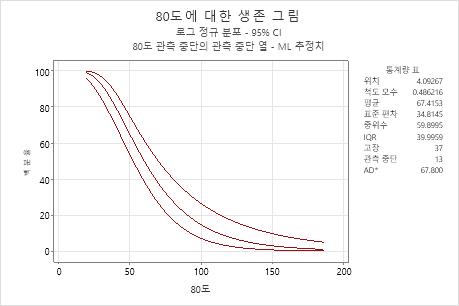
해석
엔진 와인딩 데이터의 경우 80°C 온도에서 50시간 이상 생존하는 엔진 와인딩의 확률은 약 60%입니다. 생존 함수는 위치 모수 = 4.09267이고 척도 모수 = 0.486216인 로그 정규 분포에 바탕을 두고 있습니다.
누적 고장 그림
제품이 언제 고장나는 지에 대한 측면에서 제품 신뢰도를 나타내기 위해 누적 고장 그림은 특정 시간 t까지 고장나는 항목의 누적 백분율을 표시합니다. 누적 고장 함수는 1 - 생존 함수를 나타냅니다.
- 중심선은 시간 경과에 따른 추정 누적 고장 백분율입니다.
- 오른쪽 선은 각 시점에서 누적 고장 백분율에 대한 하한을 연결합니다. 왼쪽 선은 각 시점에서 누적 고장 백분율에 대한 상한을 연결합니다.
곡선 위에 포인터를 놓으면 누적 고장 확률과 수명이 표시됩니다.
이 그림은 분포가 데이터를 잘 적합시킨 경우에만 사용해야 합니다. 선택된 분포가 데이터를 잘 적합하지 않으면 이러한 추정치가 부정확하게 됩니다. 분포가 데이터를 잘 적합하는지 여부를 확인하려면 분포 ID 그림, 확률도 및 적합도 측도를 사용합니다.
출력 예
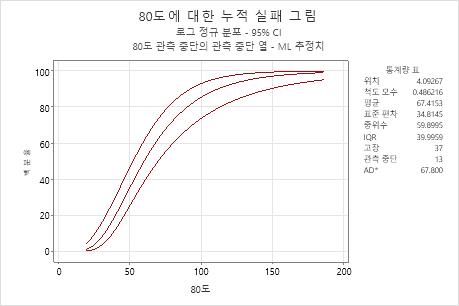
해석
엔진 와인딩 데이터의 경우 80°C 온도에서 70시간까지 고장나는 엔진 와인딩의 확률은 약 60%입니다. 누적 고장 함수는 위치 모수 = 4.09267이고 척도 모수 = 0.486216인 로그 정규 분포에 바탕을 두고 있습니다.
위험 그림
- 감소: 시간이 지남에 따라 고장날 가능성이 줄어듭니다. 감소 위험 함수는 일반적으로 제품 수명의 초기에 발생합니다.
- 일정: 일정한 비율로 고장납니다. 일정한 위험은 일반적으로 고장이 랜덤으로 발생하는 제품의 "실제 사용되는 수명" 동안에 발생합니다.
- 증가: 시간이 지남에 따라 고장날 가능성이 늘어납니다. 증가 위험은 일반적으로 제품 수명 후기에 마모에 의해 발생합니다.
위험 함수에 대한 형상 모수는 데이터와 선택된 분포에 따라 결정됩니다. 위험 곡선 위로 포인터를 놓으면 수명과 위험률에 대한 표가 표시됩니다.
이 그림은 분포가 데이터를 잘 적합하는 경우에만 사용해야 합니다. 선택된 분포가 데이터를 잘 적합하지 않으면 이러한 추정치가 부정확하게 됩니다. 분포가 데이터를 잘 적합하는지 여부를 확인하려면 분포 ID 그림, 확률도 및 적합도 측도를 사용합니다.
출력 예
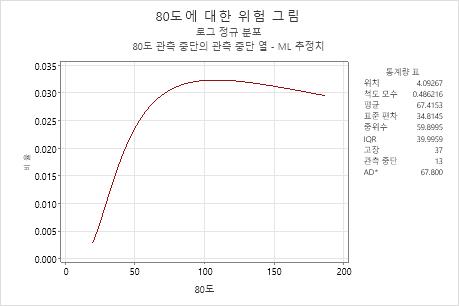
해석
엔진 와인딩 데이터의 80도 변수의 경우, 위험 함수는 위치 모수 = 4.09267이고 척도 모수 = 0.486216인 로그 정규 분포에 바탕을 두고 있습니다. 80°C 온도에서 위험률은 약 100시간까지 증가하며 그 이후 서서히 감소합니다.
다중 고장 모드 그래프
다중 고장 데이터의 경우 각 고장 모드에 대한 그래프가 표시됩니다.
- 선택된 분포가 데이터에 얼마나 잘 적합하는지 평가하려면 확률도를 사용합니다. 점이 적합선을 가깝게 따르면 해당 분포를 사용하여 데이터를 모형화합니다.
- 생존 그림을 사용하여 항목이 특정 시간까지 생존할 확률을 평가합니다. 따라서 생존도는 시간 경과에 따른 제품의 신뢰도를 표시합니다.
- 위험 함수를 사용하여 고장 우도를 단위가 지속되어 온 시간 함수(즉, 특정 시간 t에서의 순간 고장률)로 제공합니다. 위험 그림은 시간 경과에 따른 고장률의 추세를 나타냅니다.
출력 예
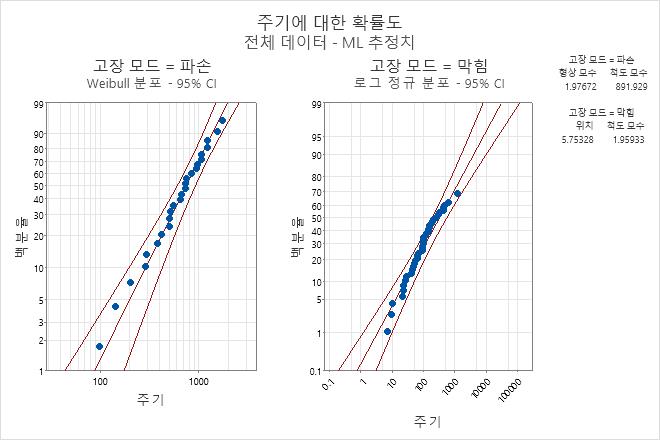
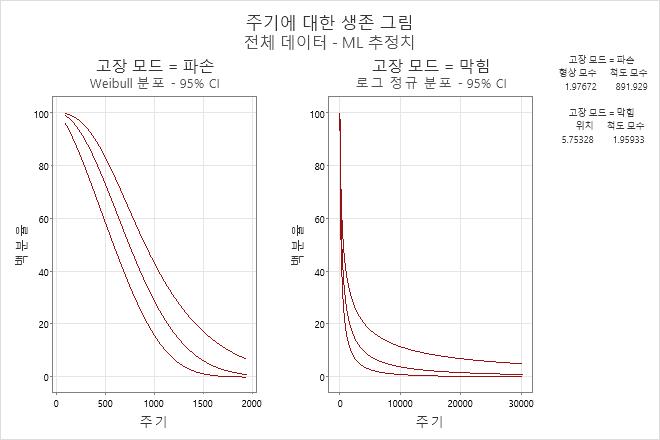
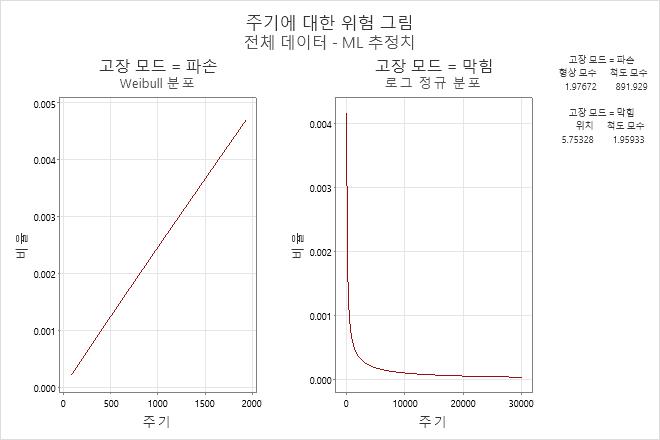
해석
- 분무관 파손의 경우 형상 모수 = 1.97672, 척도 모수 = 891.929
- 분무관 막힘의 경우 형상 모수 = 5.75328, 척도 모수 = 1.95933
분무관이 파손에 대해 200주기까지 생존할 확률은 95%이고 막힘에 대해 1500주기까지 생존할 확률은 약 20%입니다.
파손에 대한 위험률은 시간이 지남에 따라 약간씩 증가하지만 막힘의 경우 후반에는 감소합니다.
