확률도
- 표시점 - 순서가 있는 데이터 집합의 해당 확률에 대한 추정 백분위수입니다.
- 적합선 - 모수 추정치의 최대우도에 바탕을 둔 분포에서 예상되는 백분위수입니다.
- 신뢰 구간 - 백분위수에 대한 신뢰 구간입니다.
표시점은 분포에 따라 달라지지 않으므로 생성된 모든 확률도에 대해 변환 전과 동일하게 됩니다. 그러나 적합선은 선택한 모수 분포에 따라 달라집니다. 따라서 확률도를 사용하여 특정 분포가 데이터를 적합시키는지 여부를 평가할 수 있습니다. 일반적으로 적합선에 점이 가까울수록 데이터에 보다 잘 적합되는 분포입니다.
표시점
- 중위수 순위 방법(기본값)
- 수정된 Kaplan-Meier 방법
- Herd-Johnson 방법
- Kaplan-Meier 방법
데이터에 같은 수명(동일 수명)이 포함되어 있으면 모든 점(기본값), 평균(중위수) 또는 동일 수명에 대한 최대 누적 백분율이 표시됩니다. 같은 값에 고장 및 중단이 포함되어 있으면 중단 전에 고장이 발생한 것으로 간주됩니다.
이러한 각 방법은 수명을 나타내는 랜덤 변수 T에 대한 누적분포함수인 F(t)의 비모수 추정치를 생성합니다.
관측치 n개의 표본에 대해 x(1), x(2),...,x(n)을 순서 통계량 또는 가장 큰 값에서 가장 작은 값으로 정렬된 데이터로 설정합니다. 그런 다음 i는 I번째 관측치 x(I)의 순위입니다. 각 방법에 대한 공식은 다음과 같습니다.
중위수 순위(Benard의 방법)
관측 중단되지 않은 데이터에 대한 공식
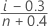
관측 중단 데이터에 대한 공식

수정된 Kaplan-Meier
관측 중단되지 않은 데이터에 대한 공식
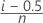
관측 중단 데이터에 대한 공식
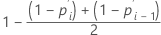
Herd-Johnson 추정치
관측 중단되지 않은 데이터에 대한 공식

관측 중단 데이터에 대한 공식
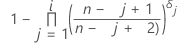
Kaplan-Meier 제품 한계 추정치
참고
가장 큰 관측치가 관측 중단되지 않은 경우 Kaplan-Meier 방법은 가장 큰 관측 중단되지 않은 관측치에 대해 p = 1이라는 결과를 낳습니다. 이 경우, 가장 큰 관측치에 대한 Kaplan-Meier 추정치는 그림에 사용할 수 없는 숫자를 생성합니다. 가장 큰 p를 이전 p와 1 간 거리의 90%로 재계산하면 이 문제가 해결됩니다.
참고
임의 관측 중단 데이터의 경우 Minitab에서는 Turnbull method1를 사용하여 누적 확률을 추정합니다.
관측 중단되지 않은 데이터에 대한 공식

관측 중단 데이터에 대한 공식
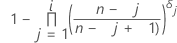
표기법
| 용어 | 설명 |
|---|---|
| i | 데이터 점의 순위(같은 값에 연속적 순위가 지정됨) |
| n | 데이터의 관측치 수 |
| δj | j번째 관측치가 관측 중단된 경우 0, j번째 관측치가 관측 중단되지 않은 경우 1 |
| ARi |
 |
| AR0 | 0과 같음 |
| p'i |
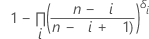 |
적합선
- Minitab에서는 Weibull 분포, 3-모수 Weibull 분포, 지수 분포, 로그 정규 분포 또는 로그 로지스틱 분포를 사용하는 경우 x-축을 로그 척도로 변환합니다.
- Minitab에서는 기본적으로 y-축을 백분율 척도로 변환합니다. y-척도 유형을 확률로 변경하면 Minitab에서 y-축을 확률 척도로 변환합니다.
| 분포 | x 좌표 | y 좌표 |
|---|---|---|
| 최소 극단값 분포 | 수명 | ln(–ln(1 – p)) |
| Weibull 분포 | ln(수명) | ln(–ln(1 – p)) |
| 3-모수 Weibull 분포 | ln(수명 – 분계점) | ln(–ln(1 – p)) |
| 지수 분포 | ln(수명) | ln(–ln(1 – p)) |
| 2-모수 지수 분포 | ln(수명 – 분계점) | ln(–ln(1 – p)) |
| 정규 분포 | 수명 | Φ –1 (p) |
| 로그 정규 분포 | ln(수명) | Φ –1 (p) |
| 3-모수 로그 정규 분포 | ln(수명 – 분계점) | Φ –1 (p) |
| 로지스틱 분포 | 수명 |
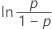 |
| 로그 로지스틱 분포 | ln(수명) |
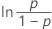 |
| 3-모수 로그 로지스틱 분포 | ln(수명 – 분계점) |
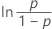 |
표기법
| 용어 | 설명 |
|---|---|
| Φ –1 | 표준 정규 분포의 역 누적분포함수 |
| ln (x) | x의 자연 로그 |
