한 신뢰도 엔지니어가 새로운 소음기 신뢰도를 평가하고 50,000마일 보증을 통해 기대할 수 있는 보증 클레임의 비율을 평가하려고 합니다. 엔지니어는 구형 및 신형 소음기 둘 다의 고장 데이터를 수집합니다. 고장 여부를 확인하기 위해 10,000마일마다 소음기를 검사했습니다.
엔지니어는 각 10,000마일 구간에 대해 고장 횟수를 기록합니다. 따라서 데이터가 임의로 관측 중단됩니다. 엔지니어는 모수 분포 분석(임의 관측 중단)을 사용하여 다음 사항을 결정합니다.
- 여러 가지 비율의 소음기에 고장이 발생할 때까지의 거리
- 50,000마일 후 생존하는 소음기의 백분율
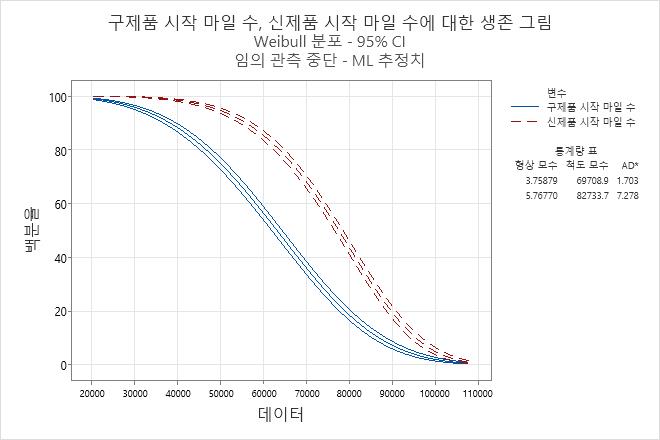
- 소음기의 생존 함수(생존 그림에 표시된 대로)
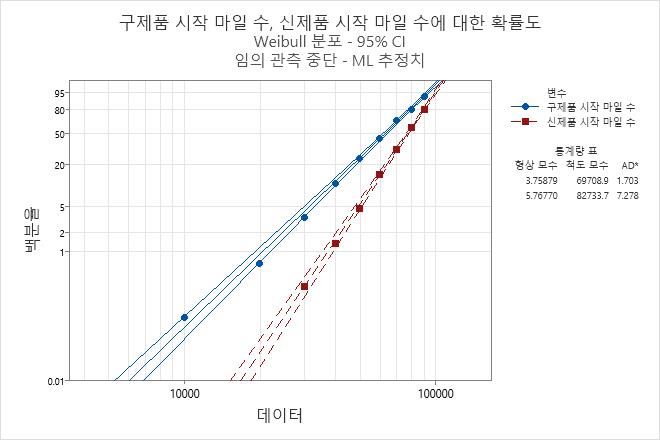
- 데이터에 대한 Weibull 분포의 적합치(확률도에 표시된 대로)
- 표본 데이터소음기신뢰성.MWX을 엽니다.
- 을 선택합니다.
- 시작 변수에 구제품 시작 마일 수신제품 시작 마일 수을 입력합니다.
- 끝 변수에 구제품 끝 마일 수신제품 끝 마일 수을 입력합니다.
- 빈도 열(옵션)에 구제품 고장 횟수신제품 고장 횟수을 입력합니다.
- 가정된 분포에서 Weibull 분포을 선택합니다.
- 추정치을 클릭합니다. 이 시간(값)에 대한 확률 추정에 50000을 입력합니다. 확인을 클릭합니다.
- 그래프을 클릭합니다. 생존 그림을 선택합니다.
- 각 대화 상자에서 확인을 클릭합니다.
결과 해석
백분위수 표를 사용하여 엔지니어는 여러 가지 비율의 이전 소음기 및 새 소음기가 고장나는 거리를 확인할 수 있습니다. 이전 소음기의 경우 소음기의 10%가 38,307마일 전까지 고장납니다. 새 소음기의 경우 소음기의 10%가 56,006.1마일 전까지 고장납니다.
생존 확률 표를 사용하여 엔지니어는 50,000마일 이상 생존할 것으로 기대되는 소음기의 비율을 확인할 수 있습니다. 이전 소음기의 경우 50,000마일 이상 생존할 확률은 약 75.07%입니다. 새 소음기의 경우 50,000마일 이상 생존할 확률은 약 94.67%입니다.
엔지니어는 생존 그림을 사용하여 여러 거리에서의 생존 확률을 확인하고, 확률도를 사용하여 Weibull 분포가 데이터를 적절하게 적합하는지 확인합니다.
- 오래된 머플러
- 변수 시작: 구제품 시작 마일 수 끝: 구제품 끝 마일 수빈도: 구제품 고장 횟수
관측 중단
관측 중단 정보 카운트 우측 관측 중단 값 83 구간 관측 중단 값 965 좌측 관측 중단 값 1 추정 방법: 최대우도법분포: Weibull 분포모수 추정치
95.0% 정규 CI 모수 추정치 표준 오차 하한 상한 형상 모수 3.75879 0.100226 3.56739 3.96045 척도 모수 69708.9 618.000 68508.1 70930.7 로그 우도 = -2083.927적합도
Anderson-Darling(수정) 1.703 분포의 특성
95.0% 정규 CI 추정치 표준 오차 하한 상한 평균(MTTF) 62963.8 585.834 61826.0 64122.5 표준 편차 18685.0 417.812 17883.8 19522.1 중위수 63232.6 618.048 62032.7 64455.6 제1 사분위수(Q1) 50042.1 692.162 48703.7 51417.3 제3 사분위수(Q3) 76037.5 658.037 74758.6 77338.2 사분위간 범위(IQR) 25995.4 610.478 24826.0 27219.9 백분위수 표
95.0% 정규 CI 백분율 백분위수 표준 오차 하한 상한 1 20501.3 730.973 19117.5 21985.2 2 24686.2 762.138 23236.7 26226.0 3 27535.4 773.441 26060.5 29093.8 4 29766.4 777.507 28280.8 31329.9 5 31630.7 778.040 30141.9 33193.0 6 33249.1 776.589 31761.3 34806.5 7 34689.8 773.926 33205.6 36240.3 8 35995.3 770.488 34516.4 37537.6 9 37194.3 766.537 35721.9 38727.5 10 38307.0 762.243 36841.8 39830.5 20 46771.7 714.662 45391.8 48193.6 30 52987.5 671.735 51687.1 54320.5 40 58301.0 638.544 57062.8 59566.1 50 63232.6 618.048 62032.7 64455.6 60 68106.3 614.500 66912.5 69321.4 70 73237.9 634.997 72003.8 74493.1 80 79117.5 693.244 77770.3 80487.9 90 87026.8 827.620 85419.8 88664.1 91 88068.9 849.547 86419.5 89749.8 92 89195.0 874.226 87497.9 90925.0 93 90425.9 902.323 88674.6 92211.8 94 91791.7 934.808 89977.7 93642.3 95 93338.0 973.162 91450.0 95265.0 96 95139.2 1019.83 93161.2 97159.2 97 97330.7 1079.31 95238.2 99469.3 98 100206 1161.47 97954.9 102508 99 104650 1296.79 102139 107223 생존 확률 표
95.0% 정규 CI 시간 확률 하한 상한 50000 0.750682 0.727911 0.771856 - 새로운 머플러
- 변수 시작: 신제품 시작 마일 수 끝: 신제품 끝 마일 수빈도: 신제품 고장 횟수
관측 중단
관측 중단 정보 카운트 우측 관측 중단 값 210 구간 관측 중단 값 839 추정 방법: 최대우도법분포: Weibull 분포모수 추정치
95.0% 정규 CI 모수 추정치 표준 오차 하한 상한 형상 모수 5.76770 0.174361 5.43589 6.11977 척도 모수 82733.7 501.285 81757.0 83722.0 로그 우도 = -1804.510적합도
Anderson-Darling(수정) 7.278 분포의 특성
95.0% 정규 CI 추정치 표준 오차 하한 상한 평균(MTTF) 76585.0 488.710 75633.1 77548.8 표준 편차 15389.5 407.421 14611.4 16209.1 중위수 77639.9 501.312 76663.5 78628.7 제1 사분위수(Q1) 66660.6 610.001 65475.7 67866.9 제3 사분위수(Q3) 87554.2 543.215 86496.0 88625.4 사분위간 범위(IQR) 20893.7 591.844 19765.3 22086.5 백분위수 표
95.0% 정규 CI 백분율 백분위수 표준 오차 하한 상한 1 37265.1 938.485 35470.3 39150.6 2 42060.6 910.590 40313.2 43883.7 3 45163.8 884.871 43462.4 46931.9 4 47516.0 861.886 45856.4 49235.7 5 49434.9 841.147 47813.5 51111.3 6 51068.9 822.219 49482.6 52706.1 7 52500.3 804.776 50946.5 54101.6 8 53779.7 788.572 52256.1 55347.7 9 54940.5 773.424 53445.3 56477.5 10 56006.1 759.186 54537.7 57514.0 20 63788.2 649.873 62527.1 65074.7 30 69192.0 576.979 68070.3 70332.1 40 73638.2 528.302 72609.9 74680.9 50 77639.9 501.312 76663.5 78628.7 60 81489.1 497.212 80520.4 82469.5 70 85439.7 519.747 84427.0 86464.5 80 89849.4 577.132 88725.4 90987.7 90 95605.5 695.279 94252.5 96978.0 91 96350.1 713.480 94961.8 97758.6 92 97151.1 733.704 95723.7 98599.9 93 98022.8 756.429 96551.4 99516.6 94 98985.2 782.340 97463.6 100530 95 100069 812.488 98488.8 101674 96 101323 848.595 99673.3 103000 97 102838 893.813 101101 104605 98 104808 955.006 102952 106696 99 107814 1053.11 105770 109898 생존 확률 표
95.0% 정규 CI 시간 확률 하한 상한 50000 0.946704 0.935996 0.955664