생존 그림 – 생명표법 추정 방법
생존 그림은 항목이 특정 시간까지 생존할 확률을 나타냅니다. 따라서 이 그림은 시간 경과에 따른 제품의 신뢰도를 표시합니다. Y-축은 생존 확률을 표시하고 X-축은 신뢰도 측도(시간, 복사지의 수, 주행 마일 등)를 표시합니다.
비모수 분석의 경우 생존 그림은 각 구간의 끝 점에 계단을 갖는 계단 함수입니다. 이 예에서 함수는 생명표법 추정 방법을 사용하여 계산됩니다.
출력 예
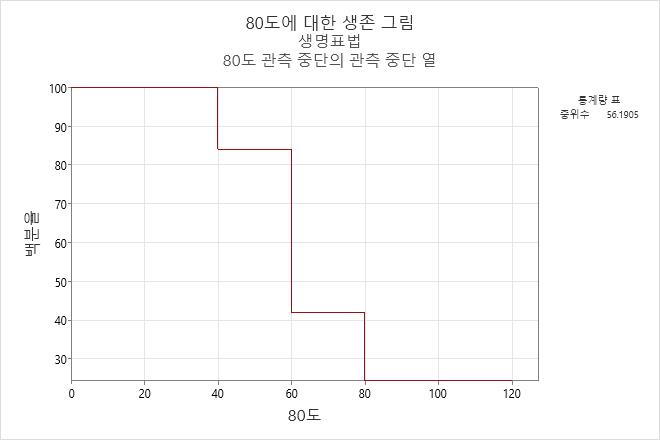
해석
80°C에서 작동하는 엔진 와인딩의 경우 와인딩이 60시간까지 생존할 확률은 0.42입니다.
누적 고장 그림 - 생명표법 추정 방법
누적 고장 그림은 품목이 특정 시간 후 고장날 확률을 나타냅니다. 따라서 이 그림은 시간 경과에 따른 제품의 고장 확률을 표시합니다. Y-축은 고장 확률을 표시하고 X-축은 신뢰도 측도(시간, 복사지의 수, 주행 마일 등)를 표시합니다.
비모수 분석의 경우 누적 고장 그림은 각 구간의 끝 점에 계단을 갖는 계단 함수입니다. 이 예에서 함수는 생명표법 추정 방법을 사용하여 계산됩니다.
출력 예
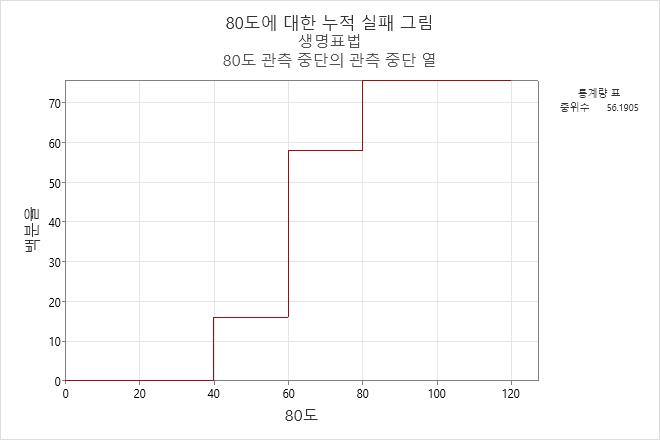
해석
80°C에서 작동하는 엔진 와인딩의 경우 와인딩이 60시간 이전에 고장날 확률은 0.58입니다.
위험 그림 - 생명표법 추정 방법
위험 함수는 고장 우도의 측도를 단위가 생존한 시간 함수로 제공합니다. 비모수 위험 그림을 사용하면 모수 추정 방법을 사용하는 경우 어떤 분포가 데이터를 모형화하기에 적합한지 확인할 수 있습니다.
비모수 분석의 경우 위험 그림은 각 구간의 중간점에 계단을 갖는 계단 함수입니다. 이 예에서 함수는 생명표법 추정 방법을 사용하여 계산됩니다.
출력 예
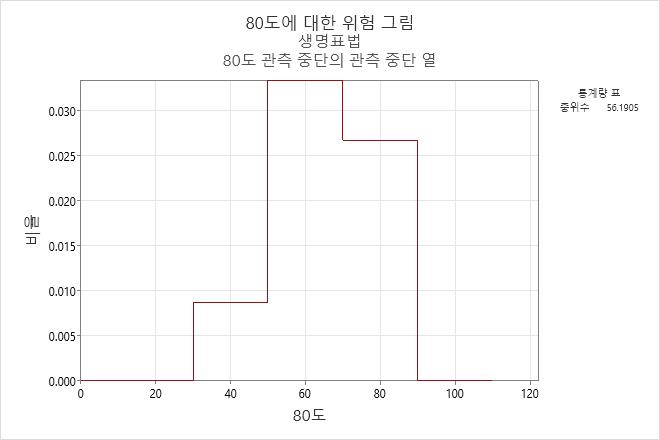
해석
80°C에서 작동하는 엔진 와인딩의 경우 위험 함수가 50 ~ 70시간 구간까지 증가하며 70시간 후 감소합니다.
다중 고장 모드 그래프 - 생명표법 추정 방법
다중 고장 데이터의 경우 각 고장 모드에 대한 그래프가 표시됩니다.
- 생존 그림을 사용하여 항목이 특정 시간까지 생존할 확률을 평가합니다. 생존도는 시간 경과에 따른 제품의 신뢰도를 표시합니다.
- 위험 함수를 사용하여 고장 우도를 단위가 생존한 시간의 함수(즉, 특정 시간 t에서의 순간 고장률)로 나타냅니다. 위험 그림은 시간 경과에 따른 고장률의 추세를 나타냅니다.
출력 예
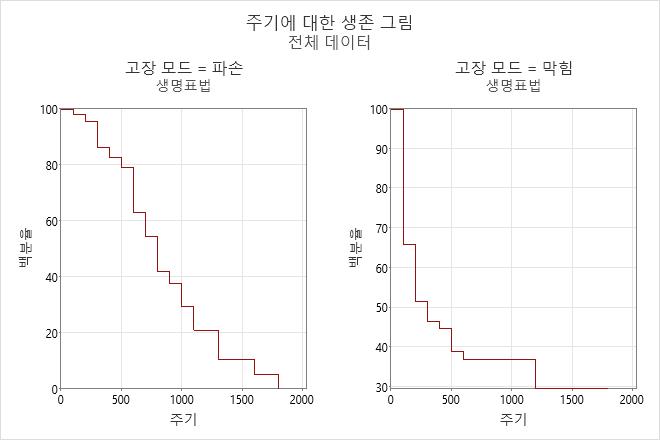
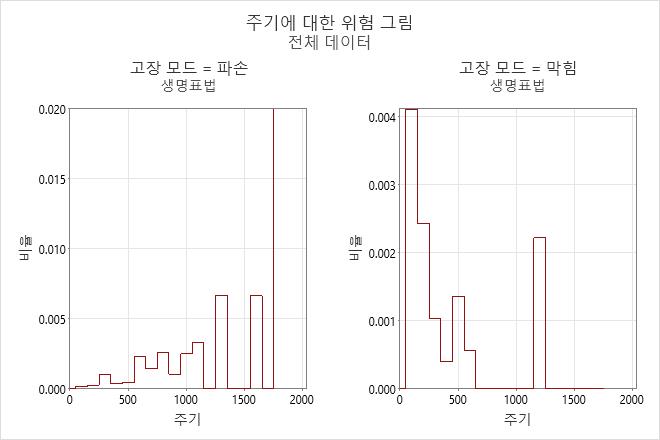
해석
식기 세척기 데이터의 경우 분무관이 파손에 대해 200주기까지 생존할 확률은 95%이고 막힘에 대해 200주기까지 생존할 확률은 51%입니다.
파손에 대한 위험률은 시간이 지남에 따라 약간씩 증가하는 것처럼 보이지만 막힘에 대한 위험률은 시간이 지남에 따라 감소하는 것처럼 보입니다.
