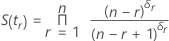
S(t0) = 1 및 t0 = 0.
경험적 위험 함수
위험 함수는 구간에 대한 고장률을 설명합니다. 첫 번째 관측 중단된 관측치 전의 위험 함수는 0입니다. 위험 함수는 관측 중단되지 않은 관측치에서만 변경됩니다. Minitab은 마지막 관측 중단되지 않은 데이터 점 후에는 위험 함수를 표시하지 않습니다.

같은 값이 있는 경우 Minitab은 같은 값에서 가장 큰 순위를 사용하여 위험 함수를 추정합니다. 자세한 내용은 Nelson1을 참조하십시오.
평균 수명
관측 중단되지 않은 데이터의 경우 평균 수명은 평균 고장 시간과 같습니다. 관측 중단 또는 관측 중단되지 않은 데이터와 함께 사용되는 일반적인 공식은 다음과 같습니다.
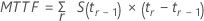
또한 가장 큰 관측치가 관측 중단된 경우 Minitab에서는 가장 큰 관측 중단되지 않은 관측치의 시간을 계산에 대한 시간 한계로 간주합니다. 자세한 내용은 Lee2를 참조하십시오.
MTTF의 표준 오차
평균 수명의 표준 오차는 분산의 제곱근입니다. 모든 관측치가 관측 중단되지 않은 경우 Minitab에서는 불편화 추정치를 계산합니다.
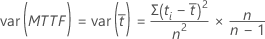
일부 데이터가 관측 중단된 경우 분산의 불편화 추정치는 다음 공식으로 계산됩니다.

경험적 위험 함수의 형상 때문에 생존 곡선 아래 영역 Ar는 높이가 생존 함수와 같고 길이가 관측 중단되지 않은 관측치 간 구간과 같은 직사각형입니다.
표기법
| 용어 | 설명 |
|---|---|
| tr | 순위가 r인 데이터 점의 시간 |
| r | 데이터 점의 순위(가장 짧은 수명의 순위가 가장 낮음) |
| n | 전체 단위 수 |
| δr | j번째 관측치가 관측 중단된 경우 0, j번째 관측치가 관측 중단되지 않은 경우 1 |
| c | 다음 관측 중단되지 않은 관측치까지 데이터 점의 수 |
| S(tr) | 시간 tr에서의 경험적 생존 함수 |
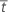 | 평균 고장 스트레스 |
| Ar | tr 오른쪽 생존 그림 곡선 아래의 영역 |
| m | 총 관측 중단되지 않은 관측치의 수 |
참고 문헌
1. W. Nelson (1982). Applied Life Data Analysis. John Wiley & Sons, Inc. 133.
2. Elisa T. Lee (1992). Statistical Methods for Survival Data Analysis, Second Edition. John Wiley & Sons, Inc. 73-76.
