한 신뢰성 공학 엔지니어가 터빈 조립 부품의 엔진 와인딩 고장률을 조사하여 와인딩에 고장이 발생하는 시간을 확인하려고 합니다. 고온에서는 와인딩이 아주 빨리 변질될 수 있습니다.
엔지니어는 80°C와 100°C에서 엔진 와인딩의 고장 시간을 기록합니다. 그러나 일부 장치는 고장이 발생하기 전에 검정에서 제거해야 합니다. 따라서 데이터가 우측 관측 중단됩니다. 엔지니어는 분포 개관 그림(우측 관측 중단)을 사용하여 대수 정규 분포를 데이터에 적합시키고 시간별 생존 및 고장률을 평가합니다.
- 표본 데이터엔진와인딩신뢰성.MWX을 엽니다.
- 을 선택합니다.
- 변수에 80도100도을 입력합니다.
- 모수 분포 분석을 선택합니다. 분포에서 로그 정규 분포을 선택합니다.
- 관측 중단을 클릭합니다. 관측 중단 열 사용 아래 80도 관측 중단100도 관측 중단을 입력합니다.
- 관측 중단 값에 0을 입력합니다.
- 각 대화 상자에서 확인을 클릭합니다.
결과 해석
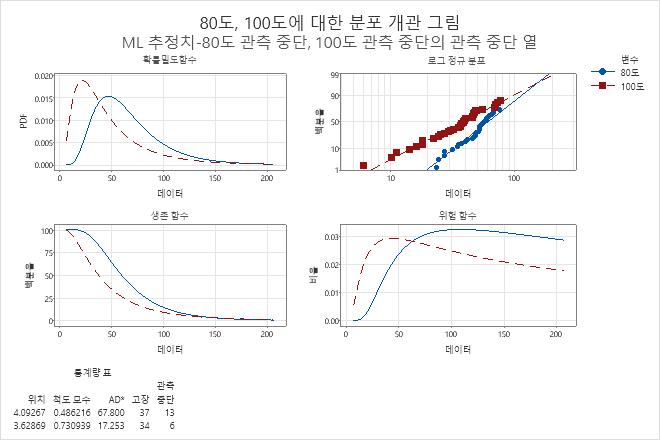
확률도는 두 변수의 경우 모두 수명에 대한 점들이 거의 직선을 이룹니다. 따라서 로그 정규 분포는 두 변수 모두에 대한 좋은 적합치입니다.
여러 변수에 대한 고장률을 비교하려면 위험 함수 그림을 사용합니다. 예를 들어, 100°C에서 초기 고장률은 80°C에서보다 크고 약 40시간에 피크(약 0.03)에 도달합니다. 80°C에서 고장률은 더 천천히 증가하며 약 50시간에 피크(0.032 이상)에 도달합니다.
여러 변수에 대한 생존율을 비교하려면 생존 함수 그림을 사용합니다. 예를 들어, 약 150시간 미만의 시간에서 생존하는 와인딩의 비율은 80°C에서 100°C에서보다 더 큽니다. 150시간 후 생존하는 와인딩의 비율은 두 온도에서 거의 같아집니다.