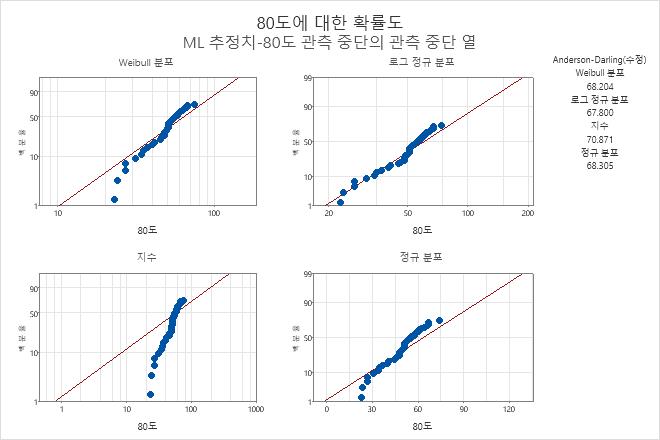
가장 적합한 분포를 선택하려면 확률도를 사용하여 공통적인 분포의 적합도를 비교합니다. 데이터 점이 확률도에서 상대적으로 직선을 형성하면 해당 분포를 사용하여 데이터를 모형화하는 것이 타당하다는 결론을 내릴 수 있습니다. 따라서 가장 적합한 분포는 점이 적합선을 매우 가깝게 따르는 분포입니다.
그림의 점은 비모수 방법을 기반으로 추정된 고장에 대한 백분위수입니다. 데이터 점에 포인터를 놓으면 관측된 수명과 추정된 누적 확률이 표시됩니다.
선은 적합된 분포에 바탕을 두고 있습니다. 이 예에서는 Weibull 분포, 로그 정규 분포, 지수 분포 및 정규 분포가 적합된 분포입니다. 적합선 위에 포인터를 놓으면 다양한 백분율에 대한 백분위수 표가 표시됩니다.
최대 우도 추정 방법(MLE)의 경우 Minitab에서는 각 분포의 적합도를 평가하기 위해 Anderson-Darling(수정) 통계량을 표시합니다.
최소 제곱(LSXY) 추정 방법을 사용하는 경우 Minitab에서는 Pearson 상관 계수를 표시합니다. 이 값은 1보다 작거나 같은 양의 수이며 값이 클수록 분포가 잘 적합된다는 것을 나타냅니다.
참고
Anderson-Darling(수정) 통계량 해석에 대한 자세한 내용은 "적합도"에서 확인하십시오.
출력 예
해석
엔진 와인딩 데이터의 경우 확률도를 살펴보면 Weibull 분포와 로그 정규 분포가 지수 분포나 정규 분포보다 데이터에 적합하다는 것을 알 수 있습니다. 로그 정규 분포가 이 데이터에 가장 적합한 것으로 보입니다.
