이 항목의 내용
신뢰도가 제공됨
시간과 신뢰도의 면에서 신뢰도 목표를 지정하면 Minitab에서는 먼저 다음 표에 지정된 분포에 대한 공식을 사용하여 시연할 모수를 계산합니다.
다음으로, Minitab에서는 실증 검사와 같은 방법으로 검사 시간 또는 표본 크기를 계산합니다.
| 분포(모수) | 시연할 모수 |
|---|---|
| Weibull 분포(척도) |
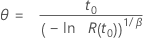 |
| 지수 분포(평균) |
 |
|
최소 극단값 분포(위치) 정규 분포(평균) 로지스틱 분포(평균) |
 |
|
로그 정규 분포(로그-위치) 로그 로지스틱 분포(로그-위치) |
 |
표기법
| 용어 | 설명 |
|---|---|
| t | 시간 |
| R(t) | 신뢰도 함수 |
| θ | 척도(Weibull 분포) 또는 평균(지수 분포) |
| β | 형상 모수(Weibull 분포) |
| σ | 척도 모수(로그 정규 분포, 로그 로지스틱 분포, 로지스틱 분포, 정규 분포, 최소 극단값 분포) |
| μ | 평균(정규 분포, 로지스틱 분포) 또는 로그-위치(로그 정규 분포, 로그 로지스틱 분포) |
| Φ-1 | 해당하는 분포의 역 누적분포함수 |
P번째 백분위수가 제공됨
P번째 백분위수(tp)의 면에서 신뢰도 목표를 지정하면 Minitab에서는 먼저 다음 표에 지정된 분포에 대한 공식을 사용하여 시연할 모수를 계산합니다.
다음으로, Minitab에서는 실증 검사와 같은 방법으로 검사 시간 또는 표본 크기를 계산합니다.
| 분포(모수) | 시연할 모수 |
|---|---|
| Weibull 분포(척도) |
 |
| 지수 분포(평균) |
 |
|
최소 극단값 분포(위치) 정규 분포(평균) 로지스틱 분포(평균) |
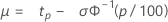 |
|
로그 정규 분포(로그-위치) 로그 로지스틱 분포(로그-위치) |
 |
표기법
| 용어 | 설명 |
|---|---|
| t | 시간 |
| R(t) | 신뢰도 함수 |
| p | 백분위수 |
| α | 척도(Weibull 분포) |
| θ | 평균(지수 분포) |
| μ | 평균(정규 분포, 로지스틱 분포), 위치(최소 극단값 분포) 또는 로그-위치(로그 정규 분포, 로그 로지스틱 분포) |
| Φ-1 | 해당하는 분포의 역 누적분포함수 |
MTTF가 제공됨
MTTF 면에서 신뢰도 목표를 지정하면 Minitab에서는 먼저 다음 표에 지정된 분포에 대한 공식을 사용하여 시연할 모수를 계산합니다.
다음으로, Minitab에서는 실증 검사와 같은 방법으로 검사 시간 또는 표본 크기를 계산합니다.
| 분포(모수) | 시연할 모수 |
|---|---|
| Weibull 분포(척도) |
 |
| 지수 분포(평균) |
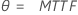 |
|
정규 분포(평균) 로지스틱 분포(평균) |
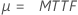 |
|
로그 정규 분포(로그-위치) |
 |
|
로그 로지스틱 분포(로그-위치) |
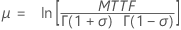 |
|
최소 극단값 분포(위치) |
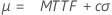 |
표기법
| 용어 | 설명 |
|---|---|
| α | 척도(Weibull 분포) |
| σ | 척도(로그 정규 분포, 로그 로지스틱 분포, 최소 극단값 분포) |
| β | 형상(Weibull 분포) |
| θ | 평균(지수 분포) |
| μ | 평균(정규 분포, 로지스틱 분포), 위치(최소 극단값 분포) 또는 로그-위치(로그 정규 분포, 로그 로지스틱 분포) |
| MTTF | 평균 수명 |
| c | Euler의 상수 ≈ 0.5772 |
| Γ | 감마 함수 |
