이 항목의 내용
분산-공분산 행렬
Var (MLE) 및 Cov (μ,σ)는 Fisher 정보 역행렬의 해당 요소에서 가져온 μ, σ, α 및 β의 MLE 분산 및 공분산입니다.
정규 분포, 로지스틱 분포 및 최소 극단값 분포에 대한 백분위수 사례
백분위수 tp를 추정하는 데 필요한 표본 크기는 다음과 같이 계산됩니다.
- 양측 신뢰 구간의 경우:
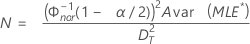
- 단측 신뢰 구간의 경우:
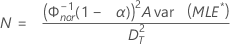
백분위수의 표준 오차 계산
분석 사양에 표본 크기가 포함된 경우 분석은 백분위수의 표준 오차를 해결합니다. 이 경우 다음 공식은 백분위수의 점근 분산을 제공합니다.
Avar(tp) = Avar(MLE*)
표기법
- tp
- 백분위수
- MLE*
- tp의 최대가능도 추정값(MLE)
- Avar(MLE*)
- 설계(또는 사용) 스트레스 수준에서 MLE의 점근 분산
- Φ-1정규 분포
- 정규 분포의 역 누적분포함수
- DT
- 백분위수에 대한 (1–α)100% 신뢰 구간 너비의 절반
Weibull 분포, 지수 분포, 로그 정규 분포 및 로그 로지스틱 분포에 대한 백분위수 사례
백분위수 tp를 추정하는 데 필요한 표본 크기는 다음과 같이 계산됩니다.
- 양측 신뢰 구간의 경우:
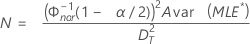
- 단측 신뢰 구간의 경우:
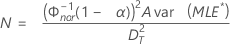


백분위수의 표준 오차 계산
분석 사양에 표본 크기가 포함된 경우 분석은 백분위수의 표준 오차를 해결합니다. 이 경우 다음 공식은 백분위수 자연 로그의 점근 분산을 제공합니다.
Avar(tp) = (tp)2Avar(ln(tp))
표기법
| 용어 | 설명 |
|---|---|
| tp | 백분위수 |
| MLE* | tp의 최대가능도 추정값(MLE) |
| Avar(MLE*) | 설계(또는 사용) 스트레스 수준에서 MLE의 점근 분산 |
| Φ-1정규 분포 | 정규 분포의 역 누적분포함수 |
| D어퍼 | 추정치와 상한 사이의 거리 |
| D하 | 추정치와 하한 사이의 거리 |
신뢰도 사례
신뢰도를 추정할 때 표준화된 시간의 MLE는 다음과 같이 계산됩니다.
- 양측 신뢰 구간의 경우:
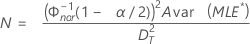
- 단측 신뢰 구간의 경우:
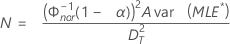
설명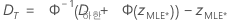
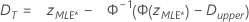
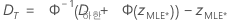
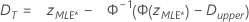
신뢰도의 표준 오차 계산
분석 규격에 표본 크기가 포함된 경우 분석은 신뢰도의 표준 오차를 해결합니다. 이 경우 다음 공식은 신뢰도의 점근 분산을 제공합니다.
Avar(신뢰도) = (φ(zMLE*))2Avar(zMLE*)
여기서 φ 의 정의는 분석의 분포에 따라 달라집니다.
| 분포 | ϕ |
|---|---|
| 정규 또는 대수 정규 분포 | 정규 분포의 pdf |
| 로지스틱 또는 로그 로지스틱 분포 | 로지스틱 분포의 pdf |
| Weibull 분포, 최소 극단값 또는 지수 분포 | 가장 작은 극단값 분포의 pdf |
표기법
| 용어 | 설명 |
|---|---|
| MLE* | 표준화 시간(ZMLE*)의 최대우도 추정치(MLE) |
| 정규 분포, 로지스틱 분포 및 최소 극단값 분포에 대한 ZMLE* | 표준화 시간 = (t − μ) / σ |
| Weibull 분포, 지수 분포, 로그 정규 분포 및 로그 로지스틱 분포에 대한 ZMLE* | 표준화 시간 = (ln(t) − μ) / σ |
| Avar(MLE*) | MLE의 점근 분산 |
| Φ-1정규 분포 | 정규 분포의 역 누적분포함수 |
| D어퍼 | 추정치와 상한 사이의 거리 |
| D하 | 추정치와 하한 사이의 거리 |
