이 항목의 내용
계수의 정의
계수는 방정식에서 변수에 곱하는 숫자입니다. 예를 들어, 방정식 y = -3.6 + 5.0X1 - 1.8X2에서 변수 X1과 X2에 곱하는 숫자 5.0과 -1.8이 계수입니다.
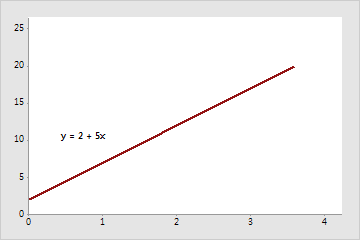
계수(및 기울기)는 양수 5입니다.
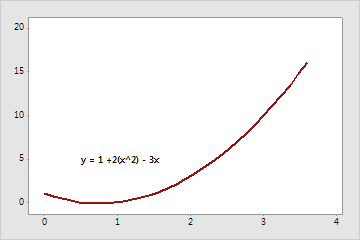
계수는 2와 -3입니다.
데이터를 모형화하기 위해 회귀 방정식을 계산할 때 표본을 바탕으로 각 예측 변수의 계수를 추정하고 이 추정치들을 계수 표에 표시합니다. 예를 들어, 회귀 방정식 결과에는 다음과 같은 계수 표가 포함됩니다.
이 방정식은 초점의 위치, 단열재 및 낮 길이에 따라 한 가정의 총 열량을 예측합니다. Minitab에서는 두 번째 열에 방정식의 계수 값을 표시합니다.
각 계수는 다른 모든 예측 변수가 상수로 고정되었을 때 X의 단위 증가에 따른 평균 반응의 변화를 추정합니다. 예를 들어, 회귀 방정식에서 북쪽 변수만 1만큼 증가하고 다른 변수들이 그대로 유지되는 경우, 총 열량은 평균적으로 약 22.95만큼 감소합니다.
계수의 p-값이 선택된 유의 수준(예: 0.05)보다 작으면 예측 변수와 반응 변수 사이에 통계적으로 유의한 관계가 있습니다. Minitab에서는 방정식의 상수 값도 계수 열에 포함됩니다.
참고
계수라는 용어는 상관 계수, 결정 계수, Kendall 계수처럼 인덱스로 사용되는 계산된 수치 값을 나타내는 데도 사용합니다.
회귀 계수에 대한 신뢰 구간 계산
신뢰 구간을 사용하여 계수 추정치의 신뢰도를 평가할 수 있습니다. 신뢰 구간이 넓을수록 추정치가 덜 정확합니다.
- 을 선택합니다.
- 대화 상자에 원하는 정보를 입력합니다.
- 결과을 클릭합니다.
- 결과 표시에서 확장된 표을 선택합니다. 그런 다음 각 대화 상자에서 확인을 클릭합니다.
참고
기본적으로, Minitab에서는 95% 양측 신뢰 구간을 계산합니다. 기본 설정을 변경하려면 을 선택한 다음 옵션을 클릭합니다. 그런 다음 신뢰 수준과 구간 유형을 입력합니다.
