계수에 대한 최대우도 추정치의 수렴을 차단하는 두 개의 조건인 완전 분리와 의사 완전 분리가 있습니다.
완전 분리
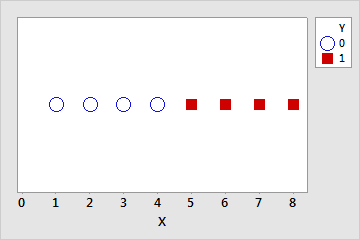
완전 분리는 예측 변수의 선형 조합이 반응 변수를 완벽하게 예측하는 경우 발생합니다. 예를 들어, 다음 데이터 집합에서 X ≤ 4이면 Y = 0입니다. X > 4이면 Y = 1입니다.
| Y | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| X | 1 | 2 | 3 | 4 | 4 | 4 | 5 | 6 | 7 | 8 |
의사 완전 분리
의사 완전 분리는 완전 분리와 유사합니다. 예측 변수가 전체가 아니라 대부분의 예측 변수 값에 대한 반응 변수를 완벽하게 예측합니다. 예를 들어, 이전 데이터 집합에서 X = 4인 값 중 하나에 대해 0 대신 Y = 1로 설정합니다. 이제 X < 4이면 Y = 0이고 X > 4이면 Y = 1이지만 X = 4이면 Y가 0 또는 1입니다. 데이터가 중간 범위에서 겹침에 따라 의사 완전 분리가 발생합니다.
| Y | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| X | 1 | 2 | 3 | 4 | 4 | 4 | 5 | 6 | 7 | 8 |

원인 및 수정
데이터 집합이 너무 작아서 사건들이 너무 낮은 확률로 관측될 때 분리가 종종 발생합니다. 모형에 예측 변수가 더 많을수록, 데이터 내의 개별 그룹들은 더 작은 표본 크기를 가지게 되므로 분리가 발생하기 더 쉽습니다.
Minitab에서는 분리가 탐지될 때 경고를 표시하지만 모형에 예측 변수가 많을수록 분리의 원인을 식별하기가 더 어렵습니다. 모형에 교호작용 항이 포함되면 훨씬 더 어렵습니다.
- 데이터 양을 늘립니다. 분리는 반응 값이 하나뿐인 예측 변수의 범주 또는 범위가 있을 때 자주 발생합니다. 표본 크기가 클수록 반응값이 여러 개일 확률이 증가합니다.
- 분리의 의미를 생각합니다. 완전 분리와 준-완전 분리는 표본 크기가 너무 작다는 것을 나타내는 반면 중요한 관계도 나타낼 수 있습니다. 특정 수준 또는 수준의 조합에서 실제 확률이 0이나 1에 가깝다면, 이는 중요한 정보입니다.
- 대체 모형을 생각합니다. 모형에 항이 더 많을수록 하나 이상의 변수에 대해 분리가 발생할 가능성이 더 높습니다. 모형에 대한 항을 선택할 때 항을 제외하는 것이 최대우도 추정치를 수렴하게 하는지 여부를 확인할 수 있습니다. 항을 제외했는데도 모형이 유용하면 그 모형을 사용하여 분석을 계속할 수 있습니다.
- 문제가 있는 변수의 범주를 합칠 수 있는지 여부를 확인합니다. 범주들을 적절하게 합치면 데이터 집합에서 분리가 없어집니다. 예를 들어, "과일"이 모형의 한 변수라고 가정합니다. 시행 횟수가 작기 때문에 "자몽"에는 사건이 없습니다. "자몽"과 "오렌지"를 "감귤류" 범주로 결합하면 분리가 없어집니다.
표 1. 완전 분리된 데이터 과일 사건 시행 자몽 0 10 오렌지 5 100 사과 25 100 바나나 40 100 표 2. 겹치는 데이터 과일 사건 시행 감귤류 5 110 사과 25 100 바나나 40 100 - 문제가 있는 범주형 변수가 집계된 변수인지 여부를 확인합니다. 집계되지 않은 변수의 반응에 대한 관계가 완전 분리를 보여주지 않는 경우 숫자 데이터를 대치하면 분리를 제거할 수 있습니다. 예를 들어, 모형에서 "고용 기간"을 집계된 변수라고 가정합니다. 데이터가 30일 단위로 증가하는 경우 최저 수준에 모든 사건이 포함되고 최고 수준에는 사건이 없습니다. 이에 따라 완전 분리가 발생합니다. 일 수를 모형으로 대치하면 분리가 제거됩니다.
표 3. 완전 분리된 데이터 기간의 범주 사건 시행 1–90 2 2 91–180 1 2 181–270 1 2 271–360 0 2 정확한 기간 사건 시행 45 1 1 60 1 1 95 1 1 176 0 1 185 0 1 241 1 1 280 0 1 299 0 1
참고 문헌
분리에 대한 자세한 내용은 Albert and J. A. Anderson (1984) "On the existence of maximum likelihood estimates in logistic regression models" Biometrika 71, 1, 1–10을 참조하십시오.
