변량 배치를 사용한 안정성 연구에 대한 방법

혼합 모형의 일반 형태

혼합 효과 모형에는 고정 효과와 랜덤 효과가 모두 포함됩니다. 혼합 효과 모형의 일반적인 형태는 다음과 같습니다.

y = Xβ + Z₁μ₁+ Z₂μ₂ + ... + Z_cμ_c + ε

표기법

혼합 모형의 특수 형태

안정성 연구는 변량 배치 요인을 사용하여 두 개의 모형을 적합합니다. 최대 모형에는 시간, 변량 배치 요인, 시간과 배치 간의 변량 교호작용이 포함됩니다.

y = Xβ + Z₁μ₁+ Z₂μ₂ + ε

더 작은 모형에는 시간과 변량 배치 요인이 포함됩니다.

y = Xβ + Z₁μ₁+ε

반응 벡터 y의 일반 분산-공분산 행렬은 다음과 같습니다.

V(σ²) = V(σ², σ²₁, ... , σ²_c) = σ²I_n + σ²₁Z₁Z'₁ + ... + σ²_cZ_cZ'_c

설명:

σ² = (σ², σ²₁, ... , σ²_c)'

σ², σ²₁, ... , σ²_c는 분산 성분이라고도 합니다.

분산에서 요인을 구분하여 혼합 모형의 로그 우도를 계산하는 H(θ)의 표현을 찾을 수 있습니다.

V(σ²) = σ²H(θ) = σ²[I_n + θ₁Z₁Z'₁ + ... + θ_cZ_cZ'_c]

배치가 변량 요인인 경우 알 수 없는 모수의 추정치는 제한된 로그 우도 함수의 음수를 두 번 최소화하여 얻어집니다. 최소화는 제한된 로그 우도 함수를 최대화하는 것과 동일합니다. 최소화하기 위한 함수는 다음과 같습니다.

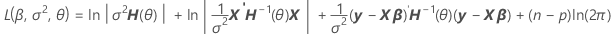
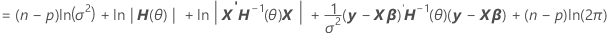
표기법

Box-Cox 변환은 아래와 같이 잔차 제곱합을 최소화하는 람다 값을 선택합니다. 결과 변환은 λ ≠ 0일 때 Y ^λ, λ = 0일 때 ln(Y)입니다. λ < 0인 경우 Minitab에서는 변환되지 않은 반응의 순서를 유지하기 위해 변환된 반응에 −1을 곱합니다.

Minitab은 -2와 2 사이의 최적 값을 검색합니다. 이 구간을 벗어나는 값의 결과는 더 적합하지 않을 수 있습니다.

Y'가 데이터 Y의 변환인 일반적인 변환의 몇 가지 예는 다음과 같습니다.

람다(λ) 값	변환
λ = 2	Y′ = Y 2
λ = 0.5	Y′ =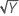
λ = 0	Y′ = ln(Y )
λ = −0.5
λ = −1	Y′ = −1 / Y

배치*시간 교호작용이 유의하면 분석에서 첫 번째 모형을 적합합니다. 교호작용이 유의하지 않지만 두 번째 모형에서 배치 항이 유의하면 분석에서 두 번째 모형을 적합합니다. 그렇지 않으면 분석에서 세 번째 모형을 적합합니다.

두 검정 모두 카이-제곱 분포에 종속되지만, 배치를 합동할 것인 지에 대한 검정은 배치를 포함하기 위한 검정과 약간 다릅니다. 검정 통계량 및 p-값에 대한 공식은 다음과 같습니다.

모형 1과 모형 2 간의 검정

차이 = −2L₂ − (−2L₁)

p = 0.5 * 확률(χ²₁ > 차이) + 0.5 * 확률(χ²₂ > 차이)

모형 2와 모형 3 간의 검정

차이 = −2L₃ − (−2L₂)

p = 0.5 * Prob(χ²₁ > 차이)

표기법

참고 문헌

1. Searle, S.R. Casella, G. and McCuloch, C.E. (1992). Variance Components
2. West, B.T., Welch, K.B. and Galecki, A.T. (2007). Linear Mixed Models: A Practical Guide Using Statistical Software.
3. Chow, S. (2007). Statistical Design and Analysis of Stability Studies.