원하는 방법 또는 공식을 선택하십시오.
적합치
예측 y 또는 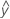 , 추정된 회귀 방정식을 사용한 주어진 예측 변수 값에 대한 평균 반응 값.
, 추정된 회귀 방정식을 사용한 주어진 예측 변수 값에 대한 평균 반응 값.
주변 적합치의 표준 오차(SE 적합치)
혼합 모형에서 주변 적합치의 표준 오차는 고정 효과에 대한 검정 방법에 따라 달라집니다. 두 방법 모두 표준 오차는 적합치 분산 행렬의 대각 원소 제곱근입니다.
Kenward-Roger의 방법

설명:
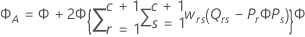
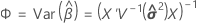
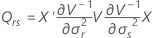
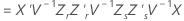
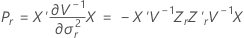
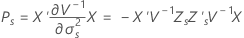
Satterthwaites 근사

설명:
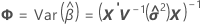
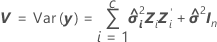
잔차
잔차는 관측치와 적합치 간의 차이입니다. 관측치의 이 부분은 적합 모형에 의해 설명되지 않습니다. 관측치의 잔차는 다음과 같습니다.
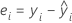
배치가 변량 요인인 경우 Minitab에서는 2가지 유형의 잔차를 계산합니다. 주변 잔차는 변량 배치에 대한 적합치를 사용하므로, 배치에 대한 계수는 방정식에 없습니다.
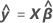
조건부 잔차는 데이터에 있는 배치에 대한 적합치를 사용합니다.
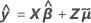
표기법
| 용어 | 설명 |
|---|---|
| yi | i번째 관측 반응 값 |
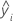 | i번째 적합 반응 값 |
 | 적합된 반응의 벡터 |
| X | 고정 효과에 대한 설계 행렬 |
 | 고정 예측 변수의 벡터 |
| Z | 변량 요인에 대한 설계 행렬 |
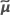 | 추정된 BLUP 값의 벡터 |
표준화 잔차
표준화 잔차는 "내적 스튜던트화 잔차"라고도 합니다.


여기서 잔차의 표준 편차는 잔차 분산 행렬의 적절한 대각 제곱근입니다.
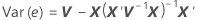
설명:
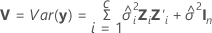
표기법
| 용어 | 설명 |
|---|---|
| ei | i번째 잔차 |
| Std(ei) | i번째 잔차의 표준 편차 |
신뢰 구간
주어진 예측 변수 값의 집합에 대해 추정된 평균 반응 값이 포함될 것으로 예상되는 범위.

혼합 모형에 있는 적합치의 표준 오차는 다음 행렬의 대각 원소의 제곱근입니다.


설명
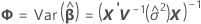
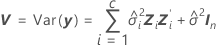
배치가 변량 요인인 경우 자유도는 다음 공식을 사용합니다.
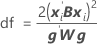
설명

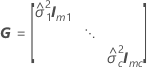
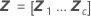
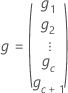

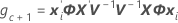
표기법
| 용어 | 설명 |
|---|---|
| t1-α/2, df | 주어진 자유도의 t 분포의 1–α/2 백분위수 |
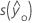 | 적합치의 표준 오차 |
| X | 설계 행렬(상수 포함) |
| X' | X의 전치 |
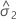 | 오차에 대한 분산 성분 |
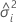 | i번째 변량 요인의 분산 성분 |
| Zi | 모형의 i번째 랜덤 효과에 대한 알려진 코드화의 n x mi 행렬 |
| Zi' | Zi의 전치 |
| In | 행과 열이 n개인 단위 행렬 |
| xi | 적합치 또는 예측에 대한 예측 변수 값 |
| W | 오차에 대한 분산 성분의 점근 분산-공분산 행렬 |
| c | 모형의 랜덤 효과 수 |
예측 구간
새 관측치의 예측 반응 값이 포함될 것으로 예상되는 범위. 예측 구간은 주변 적합치에 대한 구간을 계산하는지, 조건부 적합치에 대한 구간을 계산하는 지에 따라 다르게 계산됩니다.
주변 적합치

설명:
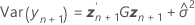

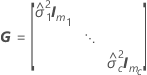
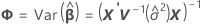
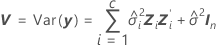
t-통계량에 대한 자유도는 다음 공식으로 계산됩니다.
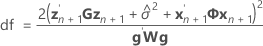
설명:
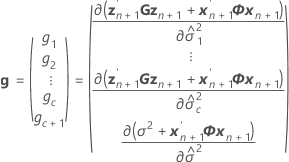


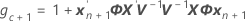
조건부 적합치

설명:
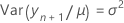
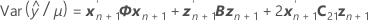
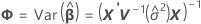
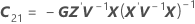
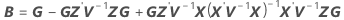
t-통계량에 대한 자유도는 다음과 같습니다.
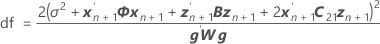
설명:
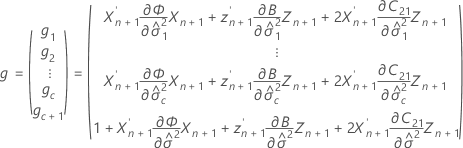

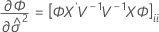
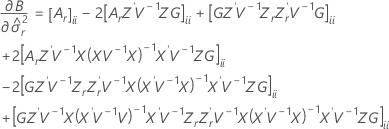
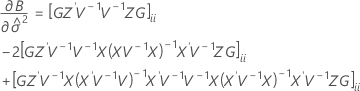
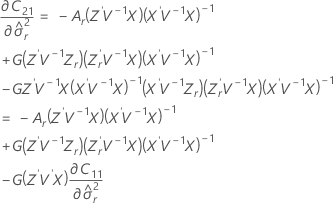
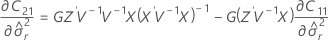
표기법
| 용어 | 설명 |
|---|---|
 | 주어진 자유도를 가진 t 분포의 1–α/2 백분위수 |
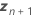 | 랜덤 예측 변수의 새 값의 벡터 |
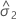 | 오차에 대한 분산 성분 |
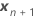 | 고정 예측 변수의 새 값의 벡터 |
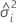 | i번째 변량 요인의 분산 성분 |
| Im | 행과 열이 m개인 단위 행렬 |
| m | 모형의 i번째 랜덤 항을 나타내기 위한 설계 행렬의 열 수 |
| c | 모형의 랜덤 효과 수 |
| Zi | 모형의 i번째 랜덤 효과에 대한 n x mi 설계 행렬 |
| Z'i | Zi의 전치 |
