원하는 방법 또는 공식을 선택하십시오.
제곱합(SS)
행렬 항에서 여러 제곱합에 대한 공식은 다음과 같습니다.



Minitab에서는 SS 회귀 분석 또는 SS 처리 성분을 순차 제곱합과 수정 제곱합을 모두 사용하여 각 항에 의해 설명되는 변동량으로 세분화합니다.
표기법
| 용어 | 설명 |
|---|---|
| b | 계수의 벡터 |
| X | 설계 행렬 |
| Y | 반응 값의 벡터 |
| n | 관측치 수 |
| J | 1의 n x n 행렬 |
Adj MS – 회귀 분석
회귀 분석의 평균 제곱(MS)에 대한 공식은 다음과 같습니다.

표기법
| 용어 | 설명 |
|---|---|
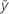 | 평균 반응 |
 | i번째 적합 반응 |
| p | 모형의 항 수 |
Adj MS – 오차
오차의 평균 제곱(MS 오차 또는 MSE로 줄이고 s2로 표기함)은 적합 회귀선 주변의 분산입니다. 공식은 다음과 같습니다.

표기법
| 용어 | 설명 |
|---|---|
| yi | i번째 관측된 반응 값 |
 | ith번째 적합 반응 |
| n | 관측치 수 |
| p | 상수를 제외한 모형 내 계수의 수 |
F
모형의 모든 요인이 고정 요인인 경우 F-통계량은 다음과 같이 가설 검정에 따라 계산됩니다.
- F(항)
-

- F(적합성 결여)
-

모형에 변량 요인이 있는 경우 F는 각 항에 대한 기대 평균 제곱을 사용하여 구성됩니다. 자세한 내용은 Neter et al.1을 참조하십시오.
표기법
| 용어 | 설명 |
|---|---|
| Adj MS 항 | 한 항이 모형의 다른 항을 설명한 후 설명하는 변동량의 측도. |
| MS 오차 | 모형이 설명하지 않는 변동의 측도. |
| MS 적합성 결여 | 모형에 항을 추가하여 모형화할 수 있는 반응의 변동 측도. |
| MS 순수 오차 | 반복된 반응 데이터의 변동 측도. |
- J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.
p-값(P)
귀무 가설을 기각하거나 받아들이는 가설 검정에서 사용됩니다. p-값은 귀무 가설이 참인 경우 최소한 실제로 계산된 값만큼 극단적인 검정 통계량을 얻을 확률입니다. 일반적으로 사용되는 p-값에 대한 컷오프 값은 0.05입니다. 예를 들어, 검정 통계량의 계산된 p-값이 0.05보다 작으면 귀무 가설을 기각합니다.
