x-점수
x-점수는 항의 선형 조합이며, 주성분 점수와 비슷합니다. x-점수는 상관 관계가 없는 열의 n × m 행렬을 구성합니다. x-점수는 PLS 성분에 대한 관측치를 투영합니다. PLS는 최소 제곱 추정 방법을 사용하여 데이터의 원래 항을 대치하는 x-점수를 적합시킵니다.
공식

표기법
| 용어 | 설명 |
|---|---|
| n | 관측치 수 |
| m | 성분 수 |
| i | 1부터 n까지의 관측치 |
| j | 1부터 p까지의 항 |
| X | 설계 행렬 |
| W | x-가중치 행렬 |
x-적재
x-적재는 주 성분 분석의 고유 벡터처럼 항을 x-점수에 연결하는 선형 계수입니다. 적재 값은 m 번째 성분에 해당하는 항의 중요성을 나타냅니다. x-적재는 p × m 행렬을 구성합니다.
공식
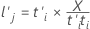
표기법
| 용어 | 설명 |
|---|---|
| p | 항 수 |
| m | 성분 수 |
| i | 1부터 n까지의 관측치 |
| j | 1부터 p까지의 항 |
| t | x-점수 |
| X | 예측 변수 |
x-가중치
x-가중치는 항과 반응 사이의 공분산을 설명합니다. 알고리즘에서 가중치는 x-점수가 직교이거나 서로 관련이 없도록 하며, x-점수를 계산하는 데 사용됩니다. x-가중치는 p × m 행렬을 구성합니다.
공식

Minitab은 벡터 길이가 1이 되도록 가중치 벡터의 척도를 정합니다.
표기법
| 용어 | 설명 |
|---|---|
| p | 항 수 |
| m | 성분 수 |
| i | 1부터 n까지의 관측치 |
| j | 1부터 p까지의 항 |
| X | x-잔차 행렬 |
| u | y-점수 |
x-잔차
x-잔차는 PLS 모형으로 설명되지 않는 예측 변수의 분산을 포함합니다. x-잔차가 상대적으로 큰 관측치는 x-공간의 특이치로, 모형으로 잘 설명되지 않음을 나타냅니다.
x-잔차는 실제 예측 변수 값과 계산된 x-값의 차이이며, 원래 예측 변수와 척도가 같습니다. x-잔차 행렬은 원래 y-행렬과 마찬가지로 n x p 행렬입니다.
x-잔차 행렬은 표준화 x-행렬로 초기화됩니다. Minitab은 m번째 성분을 계산하고 x-점수 벡터와 x-적재 벡터를 구한 후 x-잔차를 계산합니다.
공식

그런 다음 Minitab은 표준화 x-잔차를 예측 변수 값의 표준 편차로 곱하여 비표준화 x-잔차를 계산합니다.
표기법
| 용어 | 설명 |
|---|---|
| n | 관측치 수 |
| p | 항 수 |
| i | 1부터 n까지의 관측치 |
| j | 1부터 p까지의 항 |
| t | x-점수 |
| l | x-적재 |
계산된 x-값
계산된 x-값은 x-점수의 선형 조합이며, PLS 모형으로 설명되는 예측 변수의 분산을 포함합니다. 계산된 x-값이 상대적으로 작은 관측치는 x-공간의 특이치이며 모형으로 잘 설명되지 않습니다.
계산된 x-행렬은 원래 x-행렬과 마찬가지로 n x p 행렬입니다. 여기서 n은 관측치 수와 같고 p는 예측 변수의 수와 같습니다. 계산된 x-값은 예측 변수와 척도가 같습니다.
계산된 x-행렬은 영행렬로 초기화됩니다. Minitab은 m번째 성분을 계산하고 x-점수 벡터와 x-적재 부하를 구한 후 계산된 x-값을 계산합니다. 성분 수가 예측 변수의 수와 같으면 계산된 x-값은 원래 x-값과 같습니다.
공식
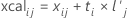
그런 다음 Minitab은 표준화된 계산된 x-값을 예측 변수 값의 표준 편차로 곱하고 평균을 더하여 비표준화된 계산된 x-값을 계산합니다.
표기법
| 용어 | 설명 |
|---|---|
| n | 관측치 수 |
| p | 예측 변수의 수 |
| i | 1부터 n까지의 관측치 수 |
| j | 1부터 p까지의 예측 변수 수 |
| t | x-점수 |
| l | x-적재 |
y-점수
y-점수는 반응 변수의 선형 결합입니다. y-점수는 n × m 행렬을 구성합니다. y-점수는 PLS 성분에 대한 관측치를 투영합니다.
공식
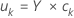
표기법
| 용어 | 설명 |
|---|---|
| n | 관측치 수 |
| m | 성분 수 |
| k | 1부터 r까지의 반응값 수 |
| Y | y 행렬 |
| c | y-적재 |
y-적재
y-적재는 반응값을 y-점수에 연결하는 선형 계수입니다. 적재 값은 m번째 성분에 해당하는 반응값의 중요성을 나타냅니다. y-적재는 r x m 행렬을 구성합니다.
공식

표기법
| 용어 | 설명 |
|---|---|
| r | 반응값 수 |
| m | 성분 수 |
| i | 1부터 n까지의 관측치 |
| k | 1부터 r까지의 반응값 |
| Y | 반응값 |
| t | x-점수 |
y-잔차
y-잔차에는 PLS 모형으로 설명되지 않는 반응값의 나머지 분산이 포함됩니다. y-잔차가 상대적으로 큰 관측치는 y-공간에서 특이치이므로 모형에 의해 잘 설명되지 않음을 알 수 있습니다.
y-잔차는 실제 반응 값과 계산된 y-값의 차이이며 원래 반응값과 척도가 같습니다. y-잔차 행렬은 원래 y-행렬과 마찬가지로 n x r 행렬입니다.
y-잔차 행렬은 처음에 표준화 Y 행렬로 설정됩니다. Minitab은 m번째 성분을 계산하고 x-점수와 y-적재 벡터를 구한 후 표준화 y-잔차를 결정합니다.
공식

그런 다음 Minitab은 표준화 y-잔차를 해당 반응 값의 표준 편차로 곱하여 비표준화 y-잔차를 계산합니다.
표기법
| 용어 | 설명 |
|---|---|
| n | 관측치 수 |
| r | 반응값 수 |
| i | 1부터 n까지의 관측치 |
| k | 1부터 r까지의 반응값 |
| t | x-점수 |
| c | y-적재 |
계산된 y-값
계산된 y-값은 x-점수의 선형 조합이며 PLS 모형으로 설명되는 반응값의 분산을 포함합니다. 계산된 y-값이 상대적으로 작은 관측치는 y-공간의 특이치이며 잘 설명되지 않습니다.
계산된 y-행렬은 원래 y-행렬과 마찬가지로 n x r 행렬입니다. 계산된 y-행렬은 처음에 영행렬로 설정됩니다. Minitab은 m번째 성분을 계산하고 x-점수와 y-적재 벡터를 구한 후 표준화된 계산된 y-값을 결정합니다.
공식

그런 다음 Minitab은 표준화된 계산된 y-값을 해당 반응값의 표준 편차로 곱하고 평균을 더하여 비표준화된 계산된 y-값을 계산합니다.
표기법
| 용어 | 설명 |
|---|---|
| n | 관측치 수 |
| r | 반응값 수 |
| i | 1부터 n까지의 관측치 |
| k | 1부터 r까지의 반응값 |
| t | x-점수 |
| c | y-적재 |
