적합치
적합치는 적합된 값 또는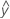 
이라고도 합니다. 적합치는 지정된 예측 변수 값에 대한 평균 반응값의 점 추정치입니다. 예측 변수 값을 x-값이라고도 합니다.
해석
적합치는 데이터 집합의 각 관측치에 대한 특정 x-값을 모형 방정식에 입력하여 계산됩니다.
예를 들어 방정식이 y = 5 + 10x이면 x-값 2에 대한 적합치는 25(25 = 5 + 10(2))입니다.
SE 적합치
적합치의 표준 오차(SE 적합치)는 지정된 변수 설정에 대해 추정된 평균 반응의 변동량을 추정합니다. 평균 반응의 신뢰 구간 계산에는 적합치의 표준 오차가 사용됩니다. 표준 오차는 항상 음수가 아닙니다.
해석
평균 반응의 추정치 정확도를 측정하려면 적합치의 표준 오차를 사용하십시오. 표준 오차가 작을수록 예측된 평균 반응이 더 정확합니다. 예를 들어 한 분석가가 배송 시간을 예측하는 모형을 개발합니다. 변수 설정 집합 하나에 대해 모형은 평균 배송 시간을 3.80일로 예측합니다. 해당 설정에 대한 적합치의 표준 오차는 0.08일입니다. 두 번째 변수 설정 집합에 대해 모형은 적합치의 표준 오차가 0.02일인 동일한 평균 배송 시간을 산출합니다. 분석가는 두 번째 변수 설정 집합의 평균 배송 시간이 3.80일에 가깝다는 것을 더 신뢰할 수 있습니다.
적합치의 표준 오차를 적합치와 함께 사용하여 평균 반응의 신뢰 구간을 생성할 수 있습니다. 예를 들어 95% 신뢰 구간은 자유도에 따라 예측 평균의 위아래로 표준 오차의 약 2배만큼 확장됩니다. 배송 시간의 경우 표준 오차가 0.08일 때 예측된 평균인 3.80일에 대한 95% 신뢰 구간은 (3.64, 3.96)일입니다. 모집단 평균이 이 범위 안에 있다고 95% 신뢰할 수 있습니다. 표준 오차가 0.02일 때 95% 신뢰 구간은 (3.76, 3.84)일입니다. 두 번째 변수 설정 집합의 신뢰 구간은 표준 오차가 더 작기 때문에 더 좁습니다.
95% CI
적합치에 대한 신뢰 구간은 예측 변수 설정이 지정된 평균 반응에 해당할 가능성이 높은 값의 범위를 제공합니다.
해석
신뢰 구간은 관측된 변수 값에 대한 적합치를 추정하는 데 사용합니다.
예를 들어 95% 신뢰 수준에서는 모형에 있는 변수의 지정된 값에 대한 모집단 평균이 신뢰 구간에 포함된다고 95% 확신할 수 있습니다. 신뢰 구간은 결과의 실제 유의성을 평가하는 데 도움이 됩니다. 해당 상황에 실제적으로 유의한 값이 신뢰 구간에 포함되는지 여부를 확인하려면 전문 지식을 이용하십시오. 신뢰 구간이 넓으면 미래 값 평균의 신뢰도가 더 낮을 수 있음을 나타냅니다. 신뢰 구간이 너무 넓어서 유의하지 않은 경우 표본 크기를 늘려보십시오.
95% PI
예측 구간(PI)은 예측 변수 값에 대한 단일 미래 반응값이 포함될 확률이 높은 범위입니다.
해석
95% 예측 구간이 있는 경우, 새로운 관측치가 구간에 포함된다는 것을 95% 신뢰할 수 있습니다. (참고: 그러나 분석의 데이터 범위에 포함된 값에 대해서만 그렇습니다.) 구간은 신뢰 수준과 예측의 표준 오차를 사용하여 계산되는 하한과 상한으로 정의됩니다. 평균 반응값에 대한 단일 반응값을 예측하는 데 불확실성이 추가되므로 예측 구간은 항상 신뢰 구간보다 넓습니다.
R-제곱 검정
검정 R2은 검정 데이터의 예측 변수 값을 사용하여 원래 모형에 의해 설명되는 반응값의 변동 비율을 나타냅니다.
검정 데이터 집합은 원래 데이터 집합과 같은 수의 예측 변수를 포함해야 합니다. 검정 데이터에 각 관측치에 대한 반응값 데이터가 있을 경우에만 검정 R2을 계산할 수 있습니다. 검정 R2은 R2과 같은 방식으로 계산됩니다.
해석
검정 R2은 PLS 모형이 검정 데이터를 얼마나 잘 예측하는지 나타냅니다. 검정 R2 값이 높을수록 모형의 예측 능력이 더 큽니다.
PLS 회귀 분석은 종종 2단계로 진행됩니다. 첫 번째 단계에서는 표본 데이터 집합(교육 데이터 집합이라고도 함)에 대해 PLS 회귀 모형을 계산하며, 교육 단계라고도 합니다. 두 번째 단계에서는 검정 데이터 집합이라고 하는 다른 데이터 집합을 사용하여 모형을 검증합니다. 반응 값이 있는 검정 데이터 집합도 있고, 반응 값이 없는 검정 데이터 집합도 있습니다. 검정 데이터 집합에 반응 값이 있으면 Minitab에서 검정 R2을 계산할 수 있습니다.
교차 검증을 사용하는 경우 검정 R2과 예측 R2을 비교해야 합니다. 이상적인 경우 두 값은 비슷합니다. 검정 R2이 예측 R2보다 상당히 작으면 교차 검증이 모형의 예측 능력에 대해 지나치게 낙관적이거나 두 데이터 표본이 다른 모집단에서 추출된 것임을 나타냅니다.
