1단계: 두 계기 또는 방법의 측정치가 서로 다른지 확인
직교 회귀 분석은 일반적으로 임상 화학 또는 실험실에서 두 기구 또는 방법이 유사한 측정값을 제공하는지 여부를 확인하기 위해 사용합니다. 상수 항에 대한 신뢰 구간에 0이 포함되어 있고 선형 항에 대한 구간에 1이 포함되어 있는 경우 일반적으로 두 기구의 측정값이 유사하다는 결론을 내릴 수 있습니다.
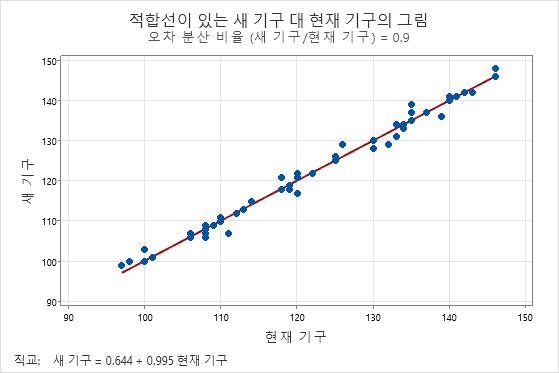
적합선이 있는 그림도 조사하여 모형이 데이터에 얼마나 적합한지 확인해야 합니다.
새 기구 = 0.644 + 0.995 현재 기구
계수
| 예측 변수 | 계수 | SE 계수 | Z | P | 근사 95% CI |
|---|---|---|---|---|---|
| 상수 | 0.64441 | 1.74470 | 0.3694 | 0.712 | (-2.77513, 4.06395) |
| 현재 기구 | 0.99542 | 0.01415 | 70.3461 | 0.000 | (0.96769, 1.02315) |
오차 분산
| 변수 | 분산 |
|---|---|
| 새 기구 | 1.07856 |
| 현재 기구 | 1.19840 |
주요 결과: 근사 95% CI
이 결과에서 상수 항에 대한 신뢰 구간은 약 (-3, 4)입니다. 구간에 0이 포함되기 때문에 분석의 이 부분에서는 두 계기의 측정치가 서로 다르다는 증거를 제시하지 않습니다.
선형 항에 대한 신뢰 구간은 약 (0.97, 1.02)입니다. 구간에 1이 포함되기 때문에 분석의 이 부분에서는 두 계기의 측정치가 서로 다르다는 증거를 제시하지 않습니다.
어떤 구간도 두 계기의 측정치가 서로 다르다는 증거를 제시하지 않기 때문에 일반적으로 계기가 유사하다는 결론을 내립니다. 적합선이 있는 그림과 잔차 그림을 조사하여 모형이 데이터에 충분히 적합한지 여부도 확인해야 합니다.
2단계: 회귀선이 데이터에 적합한지 여부 확인
- 표본에는 모든 예측 변수 값의 전체 범위에서 충분한 수의 관측치가 포함되어 있습니다.
- 표본에는 모형이 적합하지 않은 곡면성이 포함되어 있지 않습니다.
- 표본에는 결과에 중대한 영향을 미칠 수 있는 특이치가 포함되어 있지 않습니다. 특이치의 원인을 식별해 보십시오. 모든 데이터 입력이나 분별 가능한 측정 오류를 수정하십시오. 비정상적인 일회성 사건과 연관된 데이터 값을 삭제해 보십시오(특수 원인). 그런 다음 분석을 반복하십시오.
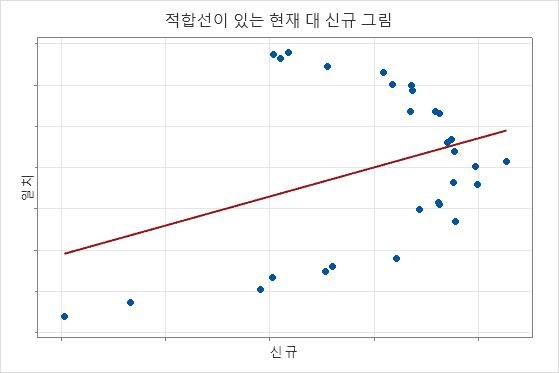
이 그림에는 서로 유사한 두 계기 또는 방법의 측정치 예제가 나와 있습니다. 점들은 선을 따르고 미미하게 흩어져 있으며, 방법 간의 체계적인 차이를 나타내는 패턴이 없습니다.
아래 결과에서 계수에 대한 신뢰 구간은 두 계기의 측정치가 서로 다르다는 증거를 제시하지 않습니다. 그러나 그림에서는 점이 선과 가까이 있지 않는 것으로 보이며, 이는 두 계기의 측정치가 유사하지 않음을 나타냅니다. 데이터가 방정식에 적합하지 않기 때문에 일반적으로 계기가 서로 다르다는 결론을 내릴 수 있습니다.
계수
| 예측 변수 | 계수 | SE 계수 | Z | P | 근사 95% CI |
|---|---|---|---|---|---|
| 상수 | -0.00000 | 0.215424 | -0.0000 | 1.000 | (-0.422224, 0.42222) |
| 신규 | 1.00000 | 0.517586 | 1.9320 | 0.053 | (-0.014450, 2.01445) |