적합선이 있는 그림
적합선이 있는 그림은 반응값과 예측 변수 데이터를 표시합니다. 이 그림에는 직교 회귀 방정식을 나타내는 직교 회귀선이 포함됩니다.
비교를 위해 최소 제곱 적합선을 그림에 표시할 수도 있습니다. 두 선의 차이가 큰 경우, 이 차이는 사용자가 예측 변수 값의 불확실성을 감안하는지 여부에 따라 결과가 얼마나 달라지는지 나타냅니다. 최소 제곱값은 직교 회귀 분석의 예측 값과 같으므로, 최소 제곱선을 사용하여 예측 값을 조사할 수도 있습니다.
해석
- 표본에는 모든 예측 변수 값의 전체 범위에서 충분한 수의 관측치가 포함되어 있습니다.
- 표본에는 모형이 적합하지 않은 곡면성이 포함되어 있지 않습니다.
- 표본에는 결과에 중대한 영향을 미칠 수 있는 특이치가 포함되어 있지 않습니다. 특이치의 원인을 식별해 보십시오. 모든 데이터 입력이나 분별 가능한 측정 오류를 수정하십시오. 비정상적인 일회성 사건과 연관된 데이터 값을 삭제해 보십시오(특수 원인). 그런 다음 분석을 반복하십시오.
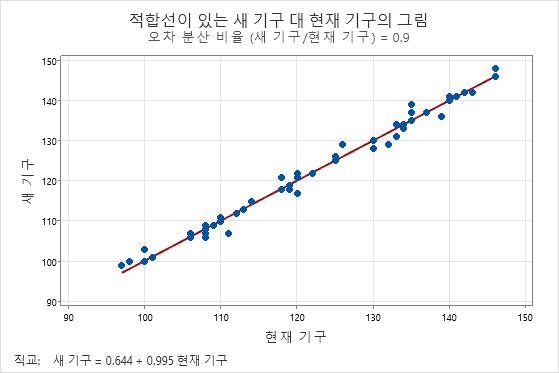
직교 회귀 분석은 종종 임상 화학 또는 실험실에서 두 계기 또는 방법이 유사한 측정치를 제공하는지 확인하기 위해 사용합니다.
이 그림에는 서로 유사한 두 계기 또는 방법의 측정치 예제가 나와 있습니다. 점들은 선을 따르고 미미하게 흩어져 있으며, 방법 간의 체계적인 차이를 나타내는 패턴이 없습니다.
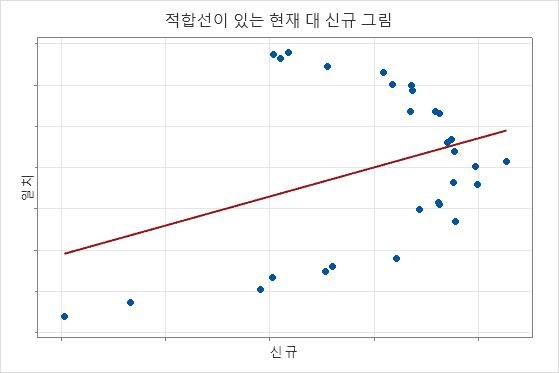
아래 결과에서 계수에 대한 신뢰 구간은 두 계기의 측정치가 서로 다르다는 증거를 제시하지 않습니다. 그러나 그림에서는 점이 선과 가까이 있지 않는 것으로 보이며, 이는 두 계기의 측정치가 유사하지 않음을 나타냅니다. 데이터가 방정식에 적합하지 않기 때문에 일반적으로 계기가 서로 다르다는 결론을 내릴 수 있습니다.
계수
| 예측 변수 | 계수 | SE 계수 | Z | P | 근사 95% CI |
|---|---|---|---|---|---|
| 상수 | -0.00000 | 0.215424 | -0.0000 | 1.000 | (-0.422224, 0.42222) |
| 신규 | 1.00000 | 0.517586 | 1.9320 | 0.053 | (-0.014450, 2.01445) |
잔차 히스토그램
잔차 히스토그램은 모든 관측치에 대한 잔차의 분포를 보여줍니다.
해석
| 패턴 | 패턴이 나타내는 내용 |
|---|---|
| 한 쪽 방향의 긴 꼬리 | 왜도 |
| 다른 막대들과 멀리 떨어져 있는 막대 | 특이치 |
직교 회귀 분석은 종종 임상 화학 또는 실험실에서 두 계기 또는 방법이 동일한 것을 측정하는지 확인하기 위해 사용합니다. 모형이 가정을 충족하지 않는 경우, 방법이 동일한 것을 측정하지 않는다는 설명이 가능합니다.
히스토그램 모양은 데이터를 그룹으로 나누는 데 사용된 구간 수에 따라 다르므로, 히스토그램을 사용하여 잔차의 정규성을 평가하지 마십시오. 그 대신 정규 확률도를 사용하십시오.
히스토그램은 데이터 점의 수가 약 20개 이상일 때 가장 효과적입니다. 표본이 너무 작으면 왜도 또는 특이치를 높은 신뢰도로 보여주기에 충분한 데이터 점이 히스토그램의 각 막대에 포함되지 않습니다.
잔차의 정규 확률도
잔차의 정규 확률도는 분포가 정규 분포일 때 잔차 대 잔차의 기대값을 표시합니다.
해석
잔차가 정규 분포를 따른다는 가정을 확인하려면 잔차의 정규 확률도를 사용하십시오. 잔차의 정규 확률도는 대략 직선을 따라야 합니다.
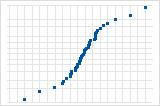
S-곡선은 긴 꼬리를 갖는 분포를 의미합니다.
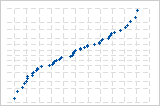
역 S-곡선은 짧은 꼬리를 갖는 분포를 의미합니다.
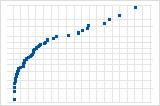
하향 곡선은 오른쪽으로 치우친 분포를 의미합니다.
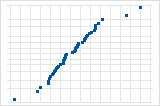
선으로부터 멀리 떨어져 있는 몇 개의 점은 특이치를 갖는 분포를 암시합니다.
직교 회귀 분석은 종종 임상 화학 또는 실험실에서 두 계기 또는 방법이 똑같은 것을 측정하는지 확인하기 위해 사용합니다. 비정규 패턴이 보이면 방법이 같은 것을 측정하지 않는다는 설명이 가능합니다. 다른 잔차 그림도 살펴보고 모형에 다른 문제(시간 순서 효과 등)가 있는지 확인하십시오. 잔차가 정규 분포를 따르지 않는 경우 신뢰 구간과 p-값이 정확하지 않을 수 있습니다.
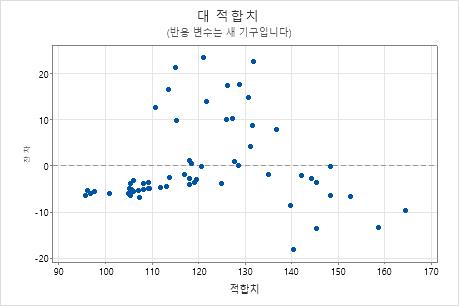
잔차 대 적합치
잔차 대 적합치 그래프는 y-축에 잔차를 표시하고 x-축에 예측 변수에 대한 적합치를 표시합니다.
직교 회귀 분석은 종종 임상 화학 또는 실험실에서 두 계기 또는 방법이 똑같은 것을 측정하는지 확인하기 위해 사용합니다. 모형이 가정을 충족하지 않는 경우, 방법이 같은 것을 측정하지 않는다는 설명이 가능합니다.
해석
잔차가 랜덤하게 분포되어 있고 잔차의 분산이 일정하다는 가정을 확인하려면 잔차 대 적합치 그림을 사용하십시오. 이상적으로는 점들이 식별 가능한 패턴 없이 0의 양쪽에 랜덤하게 분포해야 합니다.
| 패턴 | 패턴이 나타내는 내용 |
|---|---|
| 적합치에 대해 잔차가 부채꼴 모양으로 흩어져 있거나 고르지 않게 퍼져 있음 | 일정하지 않은 분산 |
| 곡선 | 고차 항 누락 |
| 한 점이 0에서 멀리 떨어져 있음 | 특이치 |
| 다른 점에서 x 방향으로 멀리 떨어져 있는 점 | 영향력 있는 점 |

특이치가 있는 그래프
점 중 하나가 나머지 모든 점보다 훨씬 더 큽니다. 따라서 그 점이 특이치입니다. 특이치가 너무 많으면 모형이 적절하지 않을 수 있습니다. 특이치의 원인을 식별해야 합니다. 모든 데이터 입력 또는 측정 오류를 수정하십시오. 비정상적인 일회성 사건과 연관된 데이터 값을 삭제해 보십시오(특수 원인). 그런 다음 분석을 반복하십시오.
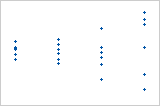
일정하지 않은 분산이 있는 그림
잔차의 분산이 적합치에 따라 증가합니다. 적합치가 증가하면 잔차 간의 산포가 더 넓어집니다. 이 패턴은 잔차의 분산이 동일하지(일정하지) 않다는 것을 나타냅니다.
잔차 대 순서
잔차 대 순서 그림은 잔차를 데이터가 수집된 순서대로 표시합니다.
해석
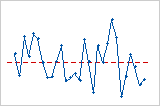
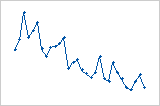
추세
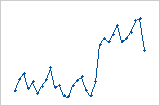
이동
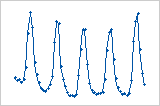
주기
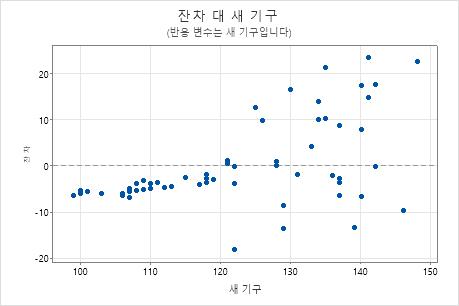
잔차 대 변수
잔차 대 변수 그림은 잔차 대 다른 변수를 표시합니다. 변수가 이미 모형에 포함되어 있을 수 있습니다. 또는 변수가 모형에 포함되어 있지 않을 수도 있지만 반응에 영향을 미칠 것으로 예상됩니다.
해석
직교 회귀 분석은 종종 임상 화학 또는 실험실에서 두 계기 또는 방법이 동일한 것을 측정하는지 확인하기 위해 사용합니다. 반응 변수 또는 예측 변수에 대한 잔차 그림의 패턴은 한 방법이 다른 방법과 어떻게 다른지 분명히 설명할 수 있습니다.
이 결과에서 잔차 대 적합치 그림은 높은 잔차가 모두 그림의 중간에 있는 패턴을 나타냅니다. 잔차 대 반응 변수 그림은 새 방법의 판독값이 커질수록 다른 방법과의 합치도가 악화됨을 분명히 보여줍니다.