원하는 방법 또는 공식을 선택하십시오.
모수 제약 조건
모수를 변환하여 모수 제한 조건을 적용합니다.1
| 조건 | 결과 |
|---|---|
| a < θ | θ = a + exp( φ ) |
| θ < b | θ = b - exp( φ ) |
| a < θ < b | θ = a +((b - a) / (1 + exp( -φ ))) |
| 용어 | 설명 |
|---|---|
| a와 b | 숫자형 상수 |
| θ's | 모수 |
| φ | 변환된 모수 |
Minitab에서는 이런 변환을 수행하고 결과를 원래 모수의 항에 표시합니다.
- Bates and Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.
모수 추정치의 표준 오차
θp 추정치의 근사 표준 오차는 S 곱하기 다음의 대각 원소 p의 제곱근입니다.  이는 다음과 같이 기록됩니다.
이는 다음과 같이 기록됩니다.

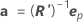

 이는 다음과 같이 기록됩니다.
이는 다음과 같이 기록됩니다.

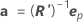

표기법
| 용어 | 설명 |
|---|---|
| n | n 번째 관측치 |
| N | 총 관측치 수 |
| p | 자유(잠금 해제된) 모수의 수 |
| R | 마지막 반복에 대한 Vi의 QR 분해에서 얻은 (상단 삼각형) R 행렬 |
| V0 | 경사 행렬 = ( ∂f(xn, θ) / ∂θp), f(x0, θ)의 부분 도함수의 P x 1 벡터, θ에서 평가됨* |
| S |
 |
모수 추정치의 상관 행렬
모수 추정치의 근사 분산-공분산 행렬은 다음과 같습니다.
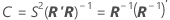
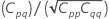

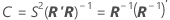
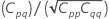

표기법
| 용어 | 설명 |
|---|---|
| R | 마지막 반복에 대한 Vi의 QR 분해에서 얻은 (상단 삼각형) R 행렬 |
| P | 자유(잠금 해제된) 모수의 수 |
| v0 | 경사 행렬 = ( ∂f(xn, θ) / ∂θp), f(x0, θ)의 부분 도함수의 P x 1 벡터, θ에서 평가됨* |
| θ | 모수 |
모수에 대한 프로파일 우도 신뢰 구간
θ = (θ1, . . . . θp)고* θ*가 θ의 마지막 반복인 경우,
우도 기반 100 (1 - α) % 신뢰 한계는 다음을 충족합니다.
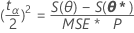
여기서 S( θp )는 θp를 일정하게 유지하고 나머지 모수에 대해 최소화할 경우에 얻어지는 SSE입니다.1 이것은 다음을 구하는 것과 같습니다.
S(θp) = S(θ*) + (tα/2)2 MSE
표기법
| 용어 | 설명 |
|---|---|
| θ | 모수 |
| n | n 번째 관측치 |
| N | 총 관측치 수 |
| P | 자유(잠금 해제된) 모수의 수 |
| tα/2 | 자유도가 N – P인 t 분포의 상위 α/2 점 |
| S(θ) | 제곱 오차의 합 |
| MSE | 평균 제곱 오차 |
- Bates and Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.
