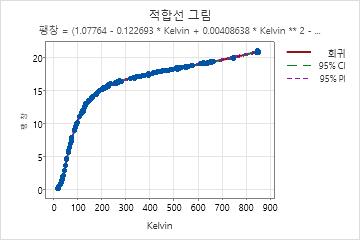
적합선 그림
비선형 모형에 하나의 예측 변수가 포함되어 있는 경우 Minitab에서는 적합선 그림을 표시하여 예측 변수와 반응 사이의 관계를 보여줍니다. 이 그림에는 회귀 방정식을 나타내는 회귀선이 포함됩니다. 또한 그림에 95% 신뢰 구간과 예측 구간을 표시할 수도 있습니다.
해석
- 표본에는 모든 예측 변수의 전체 범위에서 적절한 수의 관측치가 포함됩니다.
- 모형이 데이터의 곡면성을 적절하게 적합합니다. 데이터에 반복실험이 포함되어 있는 경우 어느 모형이 가장 적합한지 확인하려면 그림, 회귀 분석의 표준 오차(S), 적합성 결여 검정을 조사하십시오.
- 결과에 중대한 영향을 미칠 수 있는 특이치를 찾아보십시오. 특이치의 원인을 식별해 보십시오. 모든 데이터 입력 또는 측정 오류를 수정하십시오. 비정상적인 일회성 사건과 연관된 데이터 값을 삭제해 보십시오(특수 원인). 그런 다음 분석을 반복하십시오. 특이치 탐지에 대한 자세한 내용은 비정상적 관측치에서 확인하십시오.
방정식
반응과 모형의 항 간의 관계를 설명하려면 회귀 방정식을 사용합니다. 회귀 방정식은 회귀선의 대수적 표현입니다. 평균 반응 값을 계산하려면 각 예측 변수의 값을 방정식에 입력하십시오. 선형 회귀 분석과 달리 비선형 회귀 방정식 형식에는 여러 가지가 있습니다.
비선형 회귀 분석의 경우 선형 회귀 분석에 비해 각 예측 변수가 반응에 미치는 효과를 직관적으로 파악하기 어려울 수 있습니다. 선형 모형의 모수 추정치와 달리 비선형 모형의 모수 추정치에 대해서는 일관된 해석이 없습니다. 각 모수에 대한 올바른 해석은 기대 함수 및 기대 함수 내 모수의 위치에 따라 달라집니다. 비선형 모형에 하나의 예측 변수만 포함되어 있는 경우 예측 변수와 반응 사이의 관계를 확인하려면 적합선 그림을 평가하십시오.
해의 수렴이 반드시 모형 적합치가 최적이이나 오차 제곱합(SSE)이 최소라는 것을 보장하지는 않습니다. 로컬 SSE 최소값 또는 올바르지 않은 기대 함수로 인해 잘못된 모수 값에 대한 수렴이 발생할 수 있습니다. 따라서 모형 적합과 모수 값이 합리적인지 확인하려면 모수 값, 적합선 그림 및 잔차 그림을 조사하는 것이 중요합니다.
해석
이 결과에는 하나의 예측 변수와 7개의 모수 추정치가 있습니다. 반응 변수는 '팽창'이며 예측 변수는 켈빈 온도입니다. 긴 방정식이 반응 변수와 예측 변수 사이의 관계를 설명합니다. 켈빈 온도가 1도 증가할 때 구리 팽창에 미치는 영향은 시작 온도에 따라 크게 달라집니다. 온도 변경이 구리 팽창에 미치는 영향은 쉽게 요약할 수 없습니다. 예측 변수와 반응 사이의 관계를 확인하려면 적합선 그림을 평가하십시오.
켈빈 온도 값을 방정식에 입력하는 경우 구리 팽창에 대한 적합치가 산출됩니다.
방정식
(1 - 0.00576099 * Kelvin + 0.000240537 * Kelvin ** 2 - 1.23144E-07 * Kelvin ** 3)
95% CI
적합치에 대한 신뢰 구간은 예측 변수 설정이 지정된 평균 반응에 해당할 가능성이 높은 값의 범위를 제공합니다.
해석
신뢰 구간은 관측된 변수 값에 대한 적합치를 추정하는 데 사용합니다.
예를 들어 95% 신뢰 수준에서는 모형에 있는 변수의 지정된 값에 대한 모집단 평균이 신뢰 구간에 포함된다고 95% 확신할 수 있습니다. 신뢰 구간은 결과의 실제 유의성을 평가하는 데 도움이 됩니다. 해당 상황에 실제적으로 유의한 값이 신뢰 구간에 포함되는지 여부를 확인하려면 전문 지식을 이용하십시오. 신뢰 구간이 넓으면 미래 값 평균의 신뢰도가 더 낮을 수 있음을 나타냅니다. 신뢰 구간이 너무 넓어서 유의하지 않은 경우 표본 크기를 늘려보십시오.
95% PI
예측 구간은 예측 변수의 지정된 설정에서 예측 변수 값에 대한 단일 미래 반응값이 포함될 확률이 높은 범위입니다.
해석
예를 들어 한 가구 제조업체의 재료 엔지니어가 합판의 밀도를 사용하여 합판의 경도를 예측하는 단순 회귀 모형을 개발합니다. 이 엔지니어는 모형이 분석의 가정을 충족함을 확인합니다. 그런 다음, 분석가가 이 모형을 사용하여 경도를 예측합니다.
회귀 방정식에서는 새 관측치의 경도가 66.995이고 예측 구간이 [50, 85]일 것이라고 예측합니다. 이 관측치의 경도가 정확히 66.995일 확률은 낮지만, 예측 구간은 엔지니어가 실제 값이 대략 50에서 85 사이일 것이라고 95% 신뢰할 수 있음을 나타냅니다.
단일 반응 예측은 여러 반응 평균 예측보다 더 불확실하므로, 예측 구간은 항상 해당 신뢰 구간보다 넓습니다.
